题目内容
19. 如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.
如图,已知AD∥BC,AB=AC,∠BAC=90°,BD=BC,BD与AC交于E.求证:DC2=DE•DB.
分析 作AF⊥BC于F,DM⊥BC于M,由AD∥BC,得到AF=DM,根据等腰直角三角形的性质得到AF=$\frac{1}{2}$BC,得到DM=$\frac{1}{2}$BC=$\frac{1}{2}$BD,求出∠1=30°,根据等腰三角形的性质和三角形的内角和得到∠BDC=∠BCD=$\frac{180°-30°}{2}$=75°,求得∠DEC=∠1+∠ACB=30°+45°=75°=∠BCD,得到△CED∽△BCD,于是得到结论.
解答  解:如图,作AF⊥BC于F,DM⊥BC于M,
解:如图,作AF⊥BC于F,DM⊥BC于M,
∵AD∥BC,
∴AF=DM,
在Rt△ABC中,∵AB=AC,∴AF=$\frac{1}{2}$BC,
又∵DM=AF,BD=BC,
∴DM=$\frac{1}{2}$BC=$\frac{1}{2}$BD,
∴∠1=30°,
∵BC=BD,
∴∠BDC=∠BCD=$\frac{180°-30°}{2}$=75°,
∴∠DEC=∠1+∠ACB=30°+45°=75°=∠BCD,
∴△CED∽△BCD,
∴$\frac{DE}{CD}=\frac{CD}{BD}$,
∴DC2=DE•DB.
点评 本题考查了梯形的性质,相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在平面直角坐标系中,如果横坐标与纵坐标都是整数的点称为整点,将二次函数y=x2+6x-$\frac{27}{4}$的图象与x轴所围成的封闭图形染成红色,则在此红色区域内部及其边界上的整点的个数是( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
4.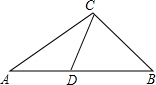 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )| A. | ∠ABC=∠ACD | B. | $\frac{BC}{AC}$=$\frac{CD}{AD}$ | C. | $\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$ | D. | ∠A=∠BCD |
 =__.
=__.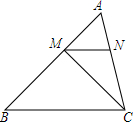 如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.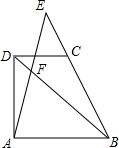 如图,梯形ABCD中,DC∥AB,点E是BC的延长线上一点,AE和BD相交于点F.若$\frac{AB}{CD}$=$\frac{3}{2}$,$\frac{BC}{BE}$=$\frac{3}{5}$,则$\frac{AE}{EF}$=$\frac{10}{19}$,$\frac{BF}{FD}$=$\frac{15}{4}$.
如图,梯形ABCD中,DC∥AB,点E是BC的延长线上一点,AE和BD相交于点F.若$\frac{AB}{CD}$=$\frac{3}{2}$,$\frac{BC}{BE}$=$\frac{3}{5}$,则$\frac{AE}{EF}$=$\frac{10}{19}$,$\frac{BF}{FD}$=$\frac{15}{4}$. 已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.
已知:如图,AB=CD,AD=BC,求证:AB∥CD,AD∥BC.