题目内容
2.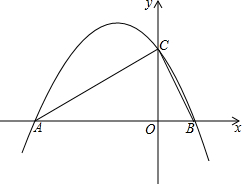 二次函数y=ax2+bx+c的图象与x轴交于点A(-8,0),B(2,0),y轴交于点C,∠ACB=90°.
二次函数y=ax2+bx+c的图象与x轴交于点A(-8,0),B(2,0),y轴交于点C,∠ACB=90°.(1)求二次函数的解析式;
(2)求二次函数的图象的顶点坐标.
分析 (1)根据相似三角形的性质求得OC的长,即可得到C的坐标,利用待定系数法求得函数的解析式;
(2)首先求得对称轴,然后代入函数解析式求得顶点坐标.
解答 解:(1)∵∠ACB=90°,OC⊥AB,
∴OC2=OA•OB=8×2=16,
则OC=4,即C的坐标是(0,4).
根据题意得:$\left\{\begin{array}{l}{64a-8b+c=0}\\{4a+2b+c=0}\\{c=4}\end{array}\right.$
解得:$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=-\frac{3}{2}}\\{c=4}\end{array}\right.$.
则二次函数的解析式是y=-$\frac{1}{4}$x2-$\frac{3}{2}$x+4;
(2)对称轴是x=$\frac{-8+2}{2}$=-3,
把x=-3代入解析式得y=$\frac{25}{4}$,
则顶点的坐标是(-3,$\frac{25}{4}$).
点评 本题考查了二次函数与x轴的交点与一元二次方程的解之间的关系,一元二次方程y=ax2+bx+c(a≠0)的解就是函数y=ax2+bx+c(a≠0)与x轴的交点的横坐标.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
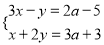 的解都为正数.
的解都为正数.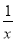 的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=
的图象有唯一公共点,若直线y=﹣x+b与反比例函数y=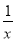 的图象有2个公共点,则b的取值范围是( )
的图象有2个公共点,则b的取值范围是( )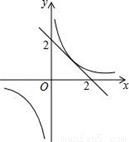
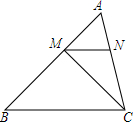 如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.
如图,△ABC中,BC=4,∠B=45°,AB=3$\sqrt{2}$,M、N分别是AB、AC上的点,MN∥BC.设MN=x,△MNC的面积为S.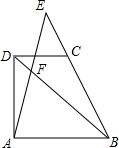 如图,梯形ABCD中,DC∥AB,点E是BC的延长线上一点,AE和BD相交于点F.若$\frac{AB}{CD}$=$\frac{3}{2}$,$\frac{BC}{BE}$=$\frac{3}{5}$,则$\frac{AE}{EF}$=$\frac{10}{19}$,$\frac{BF}{FD}$=$\frac{15}{4}$.
如图,梯形ABCD中,DC∥AB,点E是BC的延长线上一点,AE和BD相交于点F.若$\frac{AB}{CD}$=$\frac{3}{2}$,$\frac{BC}{BE}$=$\frac{3}{5}$,则$\frac{AE}{EF}$=$\frac{10}{19}$,$\frac{BF}{FD}$=$\frac{15}{4}$.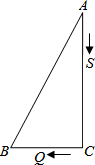 如图,△ABC中,∠C=90°,AB=5,BC=3.S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动,当其中一点到达终点时,另一点也随之停止移动.
如图,△ABC中,∠C=90°,AB=5,BC=3.S、Q两点同时分别从A、C出发,点S以每秒2个单位的速度沿着AC向点C运动,点Q以每秒1个单位的速度沿着CB向点B运动,当其中一点到达终点时,另一点也随之停止移动.