题目内容
5．
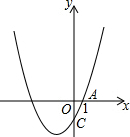如图，抛物线y=x2+2x-3与x轴正半轴，y轴分别交于点A、C，若点P在抛物线上，且△POC的面积是△AOC的面积的4倍，求点P的坐标．
分析 首先求得A的坐标，△POC的面积是△AOC的面积的4倍，据此即可求得P的横坐标，代入函数解析式即可求得P的坐标．
解答 解：令y=x2+2x-3中令y=0，则x2+2x-3=0，
解得：x1=-3，x2=1，
则A的坐标是（1，0）．
∵△POC的面积是△AOC的面积的4倍，
∴P的横坐标是4或-4．
当x=-4时，y=16-8-3=5，则P的坐标是（-4，5）；
当x=4时，y=16+8-3=21，则P的坐标是（4，21）．
故P的坐标是（-4，5）或（4，21）．
点评 本题考查了二次函数与坐标轴的交点，正确根据△POC的面积是△AOC的面积的4倍，利用A的横坐标求得P的横纵标是关键．
练习册系列答案
相关题目
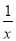+5=3y D. x=y
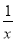的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=
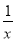的图象有2个公共点，则b的取值范围是（ ）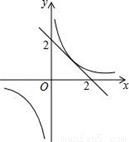
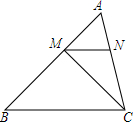如图，△ABC中，BC=4，∠B=45°，AB=3$\sqrt{2}$，M、N分别是AB、AC上的点，MN∥BC．设MN=x，△MNC的面积为S．