题目内容
15.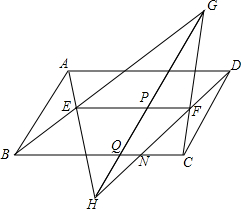 如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.
如图,已知在?ABCD内有线段EF∥BC,AE、DF的延长线交于点H,又分别交BC于点M、N,BE、CF的延长线交于点G,HG分别交EF、BC于点P、Q,求证:BQ:MQ=CQ:NQ.
分析 由四边形ABCD是平行四边形,得到AD∥BC,AD=BC,于是得到AD∥BC∥EF,推出△AHD∽△EHF,△BGC∽△EGF,根据相似三角形的性质得到$\frac{AH}{EH}$=$\frac{AD}{EF}$,$\frac{BG}{EG}$=$\frac{BC}{EF}$,根据比例的性质得到$\frac{AE}{EH}=\frac{BE}{EG}$,证得△AEB∽△HEG,得到对应角相等∠ABE=∠EGH,于是证得AB∥GH,得到GH∥CD,然后根据平行线分线段成比例和比例的性质即可得到结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵EF∥BC,
∴AD∥BC∥EF,
∴△AHD∽△EHF,△BGC∽△EGF,
∴$\frac{AH}{EH}$=$\frac{AD}{EF}$,$\frac{BG}{EG}$=$\frac{BC}{EF}$,
∴$\frac{AH}{EH}$=$\frac{BG}{EG}$,
∴$\frac{AH}{BG}=\frac{EH}{EG}$,
∵AH=EH+AE,BG=EG+BE,
∴$\frac{AH}{BG}=\frac{EH}{EG}$=$\frac{AE}{BE}$,
∴$\frac{AE}{EH}=\frac{BE}{EG}$,
∵∠AEB=∠HEP,
∴△AEB∽△HEG,
∴∠ABE=∠EGH,
∴AB∥GH,
∵AB∥CD,
∴GH∥CD,
∴$\frac{AB}{QH}=\frac{BM}{MQ}$,$\frac{CD}{QH}=\frac{CN}{NQ}$,
∴$\frac{BM}{MQ}=\frac{CN}{NQ}$,
∴$\frac{BM+MQ}{MQ}=\frac{CN+NQ}{NQ}$,
即BQ:MQ=CQ:NQ.
点评 本题考查了相似三角形的判定和性质,平行线分线段成比例定理比例的性质,平行四边形的性质,熟练掌握各定理是解题的关键.

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
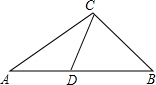 如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )
如图,点D在△ABC的边AB上,且AC2=AB•AD,则下列各式不一定成立的是( )| A. | ∠ABC=∠ACD | B. | $\frac{BC}{AC}$=$\frac{CD}{AD}$ | C. | $\frac{B{C}^{2}}{C{D}^{2}}$=$\frac{AB}{AD}$ | D. | ∠A=∠BCD |
 ;②-2是4的一个平方根;③
;②-2是4的一个平方根;③  的平方根是
的平方根是 ;④0.01的算术平方根是0.1;⑤
;④0.01的算术平方根是0.1;⑤  ,正确的有( )
,正确的有( )