题目内容
15.解方程(1)$\frac{3}{x-2}=2+\frac{x}{2-x}$;
(2)$\frac{3}{{x}^{2}-9}+\frac{x}{x-3}=1$.
分析 两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)去分母得:3=2x-4-x,
解得:x=7,
经检验x=7是分式方程的解;
(2)去分母得:3+x(x+3)=x2-9,
解得:x=-4,
经检验x=-4是分式方程的解.
点评 此题考查了解分式方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.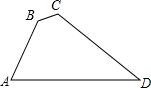 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=$\sqrt{6}$,BC=3-$\sqrt{3}$,CD=6,则AD边的长为( )| A. | $6\sqrt{3}$ | B. | $3\sqrt{3}$ | C. | $4\sqrt{2}$ | D. | $4\sqrt{3}$ |
10.下列各题中,能用平方差公式的是( )
| A. | (a-2b)(-a+2b) | B. | (-a-2b)(-a-2b) | C. | (a-2b)(a+2b) | D. | (-a-2b)(a+2b) |
5.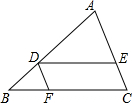 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
 如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )
如图,在△ABC中,D为AB上的一点,过点D作DE∥BC交AC于点E,过点D作DF∥AC交BC 于点F,则下列结论错误的是( )| A. | $\frac{AD}{DB}$=$\frac{DE}{BF}$ | B. | $\frac{DE}{BC}$=$\frac{AE}{AC}$ | C. | $\frac{AE}{CE}$=$\frac{BF}{CF}$ | D. | $\frac{CE}{AC}$=$\frac{BF}{BC}$ |
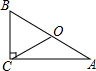 如图,Rt△ABC中,∠ACB=90°,CO是中线,延长CO到D,使DO=CO,连接AD、BD.
如图,Rt△ABC中,∠ACB=90°,CO是中线,延长CO到D,使DO=CO,连接AD、BD.
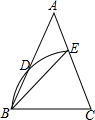 如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为21度.
如图,在△ABC中,AB=AC,∠A=32°,以点C为圆心,BC长为半径作弧,交AB于点D,交AC于点E,连结BE,则∠ABE的大小为21度.