题目内容
3.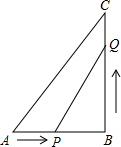 在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.
在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,一个点到达终点后,另一个点也随之停止移动,设运动的时间为x秒.(1)求AC的长度;
(2)当x为何值时,△PBQ为等腰三角形,并求PQ的长.
分析 (1)直接根据勾股定理求出AC的长即可;
(2)根据BP=6-2x,BQ=x可得出关于x的方程,求出x的值,再由勾股定理即可得出结论.
解答 解:(1)∵在Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,
∴AC=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm);
(2)∵AB=6cm,BC=8cm,P从A开始出发向点B以2cm/s的速度移动,同时点Q从点B开始出发向C以沿1cm/s的速度移动,
∴BP=6-2x,BQ=x.
∴△PBQ为等腰三角形,
∴BP=BQ,即6-2x=x,解得x=2,
∴BP=BQ=2,
∴PQ=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
14.二次函数y=-x2+bx+c的图象的最高点是(-1,-3),则b,c的值分别是( )
| A. | 2,4 | B. | 2,-4 | C. | -2,4 | D. | -2,-4 |

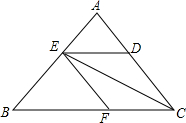 如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.
如图,点D、E、F分别是△ABC的边AC、AB、BC上的点,且DE∥BC,EF∥AC,且CE是△ABC的角平分线,求证:CE是∠DEF的平分线.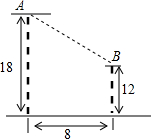 如图,要在两幢楼房的房顶A、B间拉一根光缆线(按线段计算),则至少10米.
如图,要在两幢楼房的房顶A、B间拉一根光缆线(按线段计算),则至少10米.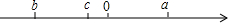 已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.
已知有理数a、b、c在数轴上对应的点如图所示,且表示数a的点、数b的点与原点的距离相等.