Question

13．如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．
（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．
（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．

Answer 1

分析 （1）延长AP后通过外角定理可得出结论；
（2）延长BA到E，延长DC到F，利用内角和定理解答．

解答 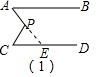证明：（1）∠P=∠A+∠C，
如图（1）延长AP交CD与点E．
∵AB∥CD，
∴∠A=∠AEC．
又∵∠APC是△PCE的外角，
∴∠APC=∠C+∠AEC．
∴∠APC=∠A+∠C；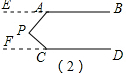

（2）∠P=360°-（∠A+∠C）．
如图（2）延长BA到E，延长DC到F，
由（1）得∠P=∠PAE+∠PCF．
∵∠PAE=180°-∠PAB，∠PCF=180°-∠PCD，
∴∠P=360°-（∠PAB+∠PCD）．

点评 本题考查平行线的性质，难度不大，注意图形的变化带来的影响，不要有惯性思维．