题目内容
15. 如图,已知AB∥CD,BC平分∠ABE,∠C=36°,则∠BED的度数是( )
如图,已知AB∥CD,BC平分∠ABE,∠C=36°,则∠BED的度数是( )| A. | 18° | B. | 36° | C. | 58° | D. | 72° |
分析 根据平行线的性质得到∠ABC=∠C=36°,再根据角平分线的定义得到∠ABC=∠EBC=36°,然后利用三角形外角性质计算即可.
解答 解:∵AB∥CD,
∴∠ABC=∠C=36°,
又∵BC平分∠ABE,
∴∠ABC=∠EBC=36°,
∴∠BED=∠C+∠EBC=36°+36°=72°.
故选D.
点评 本题考查了平行线的性质:两直线平行,内错角相等.也考查了三角形外角性质以及角平分线的定义.

练习册系列答案
相关题目
4.下列方程①x2-2x-1=0;②ax2+bx+c=0;③$\frac{1}{{x}^{2}}$+3x-5=0;④-x2=0;⑤(x-1)2+y2=2;⑥(x-1)(x-3)=x2,其中一元二次方程共有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.在下列表述中,能确定位置的是( )
| A. | 北偏东30° | B. | 距学校500m的某建筑 | ||
| C. | 东经92°,北纬45° | D. | 某电影院3排 |
 在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.
在Rt△EDF中,ED+DF=10,ED=EG,FD=FH.求△HDG外接圆的半径的最大值.
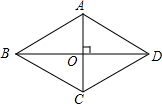 如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可)
如图,四边形ABCD的对角线互相垂直,且满足AO=CO,请你添加一个适当的条件AC、BD互相平分(答案不唯一),使四边形ABCD成为菱形(只需添加一个即可)