Question

16．如图，△ABC和△DEC是等边三角形
（1）画出△DEC绕点C顺时针旋转120°的△D′E′C′；
（2）连接BD′交AC于点M，连接AE′交CD′于点N，写出图中所有的全等三角形．

Answer 1

分析 （1）根据旋转方向，旋转角度和旋转中心，进行画图即可；
（2）根据旋转可得旋转前后的三角形全等，根据等边三角形的性质，可判定△BCD'≌△ACE'，再根据全等三角形的性质得出对应角相等，进而判定△BCM≌△ACN，△D'CM≌△E'CN即可．

解答 解：（1）如图所示，△D′E′C′即为所求；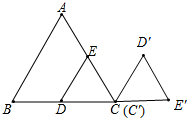

（2）如图，根据旋转可得：△CDE≌△C'D'E'，
由BC=AC，∠BCD=∠ACE'=120°，D'C=E'C可得：△BCD'≌△ACE'，
∴∠CBM=∠CAN，
又∵∠BCM=∠ACN=60°，BC=AC，
∴△BCM≌△ACN，
同理可得：△D'CM≌△E'CN，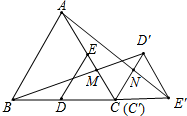

点评 本题主要考查了利用旋转变换进行作图以及等边三角形的性质，根据旋转的性质可知，通过作相等的角，在角的边上截取相等的线段的方法找到对应点，再顺次连接得出旋转后的图形．