题目内容

11．一个圆柱形铁桶的底面半径为12cm，高为32cm，则桶内所能容下的木棒最长为（　　）
A．20cmB．50cmC．40cmD．45cm

分析 根据题意画出示意图，AC为圆桶底面直径，AC=24cm，CB=32cm，那么线段AB的长度就是桶内所能容下的最长木棒的长度，在直角三角形ABC中利用勾股定理即可求出AB，也就求出了桶内所能容下的最长木棒的长度．

解答 解：如图，AC为圆桶底面直径，
∴AC=2×12=24cm，CB=32cm，
∴线段AB的长度就是桶内所能容下的最长木棒的长度，
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2{4}^{2}+3{2}^{2}}$=40cm．
故桶内所能容下的最长木棒的长度为40cm．
故选C．

点评 本题考查勾股定理的实际应用，首先要正确理解题意，明白怎么放桶内所能容下的木棒最长，然后灵活利用勾股定理，难度一般．

练习册系列答案
相关题目
14．数轴上点A所表示数的数是-5，点B到点A的距离是5，则点B所表示的数是0或-10．
15．用文字叙述下列代数式的意义：
（1）2（|a|+3）表示a的绝对值与3的和的2倍；（2）$\frac{3}{x-y}$表示3与x-y的差的商；
（3）$\frac{1}{m}$-$\frac{1}{n}$表示m的倒数与n的倒数的差；（4）$\frac{1}{4}$（a+b）-c2表示a与b的和的四分之一与c的平方的差．
12．在三角形MNQ中．
（1）如图1，求证：∠M+∠N+∠Q=180°；
（2）如图2，当MP∥NQ，且∠PMQ=90°-$\frac{1}{2}$∠NMQ．求证：∠N=∠MQN；
（3）在（2）的条件下，如图3，在MN的延长线上取一点K，连接KQ交MP于点G，且2KG=KQ，2∠MKG=∠NMQ，过点K，作RK⊥NK，交直线NQ于点R，若KN=15，KR=20，NR=25，QR=16，在直线MP上有一点B，在直线NQ上有一点A，当△ABQ和△KNQ的面积相等时．求线段AN的长．
6．如图，在平面直角坐标系xOy中，边长为2的正方形OCBA，点A、C分别在x轴、y轴上，把正方形绕点O逆时针旋转α 度后得到正方形OC1B1A1（ 0＜α＜90）﹒
（1）直线OB的表达式是y=x；
（2）在直线OB上找一点P（原点除外），使△PB1A1为等腰直角三角形，则点P的坐标是（2$\sqrt{2}$，2$\sqrt{2}$），（$\sqrt{10}$，$\sqrt{10}$），（$\sqrt{5}$，$\sqrt{5}$）．
16．如图，在△ABC中，∠B=70°，∠BAC=45°，AD⊥BC于点D，则∠CAD的度数为25°．
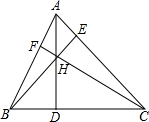3．如图，AD为锐角△ABC的高线（AC＞AB），H为线段AD上一点，连结BH，CH并延长分别交三角形的边于点E，F，且∠ABE=∠ACF，求证：H为△ABC的垂心．
20．一个两位数，个位数字与十位数字的和为6，设十位数字为x，则这个两位数可表示为9x+6．
1．抛物线y=x2向左平移8个单位，再向下平移9个单位后，所得抛物线的表达式是（　　）
A．y=（x+8）2-9B．y=（x-8）2+9C．y=（x-8）2-9D．y=（x+8）2+9

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网