题目内容
阅读下列材料:
在平面直角坐标系中,若点P1(x1,y1)、P2(x2,y2),则P1、P2两点间的距离为
.例如:若
P1(3,4)、P2(0,0),则P1、P2两点间的距离为
=5.
设⊙O是以原点O为圆心,以1为半径的圆,如果点P(x,y)在⊙O上,那么有等式
=1,即x2+y2=1成立;反过来,如果点P(x,y)的坐标满足等式x2+y2=1,那么点P必在⊙O上,这时,我们就把等式x2+y2=1称为⊙O的方程.
在平面直角坐标系中,若点P0(x0,y0),则P0到直线y=kx+b的距离为
.
请解答下列问题:
(I)写出以原点O为圆心,以r(r>0)为半径的圆的方程.
(II)求出原点O到直线y=
-
的距离.
(III)已知关于x、y的方程组:
,其中n≠0,m>0.
①若n取任意值时,方程组都有两组不相同的实数解,求m的取值范围.
②当m=2时,记两组不相同的实数解分别为(x1,y1)、(x2,y2),
求证:(x1-y1)2+(x2-y2)2是与n无关的常数,并求出这个常数.
在平面直角坐标系中,若点P1(x1,y1)、P2(x2,y2),则P1、P2两点间的距离为
| (x1-x2)2+(y1-y2)2 |
P1(3,4)、P2(0,0),则P1、P2两点间的距离为
| (3-0)2+(4-0)2 |
设⊙O是以原点O为圆心,以1为半径的圆,如果点P(x,y)在⊙O上,那么有等式
| x2+y2 |
在平面直角坐标系中,若点P0(x0,y0),则P0到直线y=kx+b的距离为
| |kx0-y0+b| | ||
|
请解答下列问题:
(I)写出以原点O为圆心,以r(r>0)为半径的圆的方程.
(II)求出原点O到直线y=
| (1-n2)x |
| 2n |
| 1+n2 |
| 2n |
(III)已知关于x、y的方程组:
|
①若n取任意值时,方程组都有两组不相同的实数解,求m的取值范围.
②当m=2时,记两组不相同的实数解分别为(x1,y1)、(x2,y2),
求证:(x1-y1)2+(x2-y2)2是与n无关的常数,并求出这个常数.
考点:一次函数综合题
专题:
分析:(I)仿照题意,可列出以原点O为圆心,以r(r>0)为半径的圆的方程,表示到原点(0,0)距离是r的点;
(II)由点P0(x0,y0)到直线y=kx+b的距离公式为
,代入公式即可求解;
(III)①x2+y2=m,表示以原点为圆心,半径是
的圆,y=
-
表示直线,当直线与y轴的交点到圆心的距离小于圆的半径时,方程组都有两组不相同的实数解,由此求m的取值范围;
②(x1-y1)2+(x2-y2)2表示:两个交点之间的距离,两交点之间的线段就是圆的直径,据此即可判断.
(II)由点P0(x0,y0)到直线y=kx+b的距离公式为
| |kx0-y0+b| | ||
|
(III)①x2+y2=m,表示以原点为圆心,半径是
| m |
| (1-n2)x |
| 2n |
| 1+n2 |
| 2n |
②(x1-y1)2+(x2-y2)2表示:两个交点之间的距离,两交点之间的线段就是圆的直径,据此即可判断.
解答:解:(I)以原点O为圆心,以r(r>0)为半径的圆的方程是:x2+y2=r2;
(II)k=
,
则求出原点O到直线y=
-
的距离是:
=1;
(III)①∵1+n2≥2n,则
≥
≥1,
即直线y=
-
与y轴的交点的纵坐标一定在(0,1)和(0,-1)之间.
x2+y2=m,表示以原点为圆心,半径是
的圆.
∵方程组都有两组不相同的实数解,
∴
>1,
∴m>1;
②证明:∵(x1-y1)2+(x2-y2)2表示:两个交点之间的距离,两交点之间的线段就是圆的直径.
∴(x1-y1)2+(x2-y2)2=2
,则与n的值无关,
∴次常数为2
.
(II)k=
| 1-n2 |
| 2n |
则求出原点O到直线y=
| (1-n2)x |
| 2n |
| 1+n2 |
| 2n |
|-
| ||||
|
(III)①∵1+n2≥2n,则
| 1+n2 |
| 2n |
| 2n |
| 2n |
即直线y=
| (1-n2)x |
| 2n |
| 1+n2 |
| 2n |
x2+y2=m,表示以原点为圆心,半径是
| m |
∵方程组都有两组不相同的实数解,
∴
| m |
∴m>1;
②证明:∵(x1-y1)2+(x2-y2)2表示:两个交点之间的距离,两交点之间的线段就是圆的直径.
∴(x1-y1)2+(x2-y2)2=2
| m |
∴次常数为2
| m |
点评:本题是阅读理解的问题,关键是理解题目叙述的意义,能从图形的观点认识方程,方程组,考查了数形结合的思想方法.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
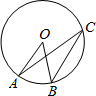 如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )
如图,点O是⊙O的圆心,点A、B、C在⊙O上,AO∥BC,∠AOB=40°,则∠OAC的度数等于( )| A、40° | B、60° |
| C、50° | D、20° |
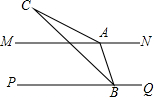 如图,MN∥PQ,A、B分别在MN、PQ上,∠ABP=70°,BC平分∠ABP,且∠CAM=20°,则∠C的度数为
如图,MN∥PQ,A、B分别在MN、PQ上,∠ABP=70°,BC平分∠ABP,且∠CAM=20°,则∠C的度数为 如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
如图,在△ABC中,∠B=60°,AB=10,BC=12,则边AC=
 如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为
如图,草坪上的自动喷水装置能旋转220°,若它的喷射半径是20m,则它能喷灌的草坪的面积为