题目内容
2.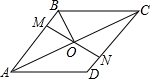 如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.
如图,在菱形ABCD中,M、N分别在AB、CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为62°.
分析 根据菱形的性质以及AM=CN,利用ASA可得△AMO≌△CNO,可得AO=CO,然后可得BO⊥AC,继而可求得∠OBC的度数.
解答 解:∵四边形ABCD为菱形,
∴AB∥CD,AB=BC,
∴∠MAO=∠NCO,∠AMO=∠CNO,
在△AMO和△CNO中,
$\left\{\begin{array}{l}{∠MAO=∠NCO}\\{AM=CN}\\{∠AMO=∠CNO}\end{array}\right.$
∴△AMO≌△CNO(ASA),
∴AO=CO,
∵AB=BC,
∴BO⊥AC,
∴∠BOC=90°,
∵∠DAC=28°,
∴∠BCA=∠DAC=28°,
∴∠OBC=90°-28°=62°.
故答案为:62°.
点评 本题考查了菱形的性质和全等三角形的判定和性质,注意掌握菱形对边平行以及对角线相互垂直的性质.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
15.下列命题中:①4的平方根是±2;②16的算术平方根是2;③若x2=9,则x=3;④若x3=-8,则x=-2.其中是真命题的有( )
| A. | ①② | B. | ①④ | C. | ①②③ | D. | ①②④ |
16.正五边形的一个内角的度数为( )
| A. | 100° | B. | 108° | C. | 112° | D. | 120° |
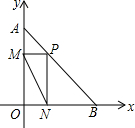 如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.
如图,点A(0,4),点B(3,0),点P为线段AB上一个动点,作PM⊥y轴于点M,作PN⊥x轴于点N,连接MN,则MN的最小值为$\frac{12}{5}$.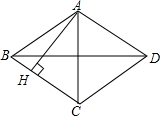 菱形ABCD的对角线AC=6cm,BD=8cm,AH⊥BC于H,则AH的长是$\frac{24}{5}$cm.
菱形ABCD的对角线AC=6cm,BD=8cm,AH⊥BC于H,则AH的长是$\frac{24}{5}$cm.