题目内容
16.在正方形ABCD中,BD是一条对角线,点P在CD上(与点C、D不重合),连接AP,平移△ADP,使点D移动到点C,得到△BCQ,过点Q作QH⊥BD于H,连接AH,PH.(1)依题意补全图1;
(2)求证;PQ=AD;
(3)判断AH与PH的关系与位置关系并加以证明.
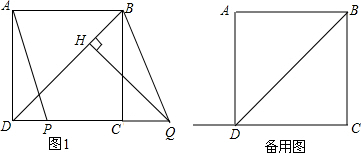
分析 (1)根据题意画出图形即可;
(2)根据平移△ADP,使点D移动到点C,得到△BCQ,即△ADP≌△BCQ,即可得到DP=CQ,证明CD=PQ,由四边形ABCD为正方形,所以AD=CD,即可得到PQ=AD.
(3)AH=PH,AH⊥PH,连接CH,先根据正方形的性质得出△DHQ是等腰直角三角形,再由SAS定理得出△HDP≌△HQC,故PH=CH,∠HPC=∠HCP,由正方形的性质即可得出结论.
解答 解:(1)如图1,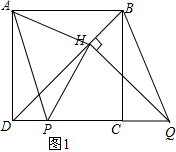
(2)∵平移△ADP,使点D移动到点C,得到△BCQ,
∴△ADP≌△BCQ,
∴DP=CQ,
∵DP+PC=DC,CQ+PC=PQ
∴CD=PQ,
∵四边形ABCD为正方形,
∴AD=CD,
∴PQ=AD.
(3)AH=PH,AH⊥PH,如图2,连接CH,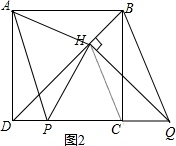
∵四边形ABCD是正方形,QH⊥BD,
∴∠HDQ=45°,
∴△DHQ是等腰直角三角形.
∵DP=CQ,
在△HDP与△HQC中,
$\left\{\begin{array}{l}{DH=QH}\\{∠HDP=∠HQC}\\{DP=QC}\end{array}\right.$,
∴△HDP≌△HQC(SAS),
∴PH=CH,∠HPC=∠HCP.
∵BD是正方形ABCD的对称轴,
∴AH=CH,∠DAH=∠HCP,
∴∠AHP=180°-∠ADP=90°,
∴AH=PH,AH⊥PH.
点评 本题考查的是四边形综合题,涉及到正方形的性质、图形平移的性质、全等三角形的判定与性质等知识,难度适中,解决本题的关键是熟记全等三角形的性质定理和判定定理.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
6.因为$\frac{3}{4}$a=1,所以( )
| A. | $\frac{3}{4}$是倒数 | B. | a是倒数 | C. | $\frac{3}{4}$和a都是倒数 | D. | $\frac{3}{4}$和a互为倒数 |
7.下列交换加数位置的变形中,正确的是( )
| A. | 1-4+5-4=1-4+4-5 | |
| B. | 4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 | |
| C. | 1-2+3-4=2-1+4-3 | |
| D. | -$\frac{1}{3}$+$\frac{3}{4}$-$\frac{1}{6}$-$\frac{1}{4}$=$\frac{1}{4}$+$\frac{3}{4}$-$\frac{1}{3}$-$\frac{1}{6}$ |
1.若有理数a满足a-|a|=2a,则a的取值范围是( )
| A. | a>0 | B. | a<0 | C. | a≥0 | D. | a≤0 |
 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图:
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图: 如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.
如图二次函数y=ax2+bx+c的部分图象及顶点坐标(-1,-3.2),由图象可知关于x的方程ax2+bx+c=0的两根x1=1.3,x2=-3.3.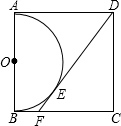 正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.
正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.