题目内容
15. 在△ABC中,∠B=50°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数.
在△ABC中,∠B=50°,∠C=60°,AD是高,AE是角平分线,求∠EAD的度数.
分析 根据三角形的内角和定理得出∠BAC,再根据角平分线的定义∠BAE,根据外角的性质得出∠AED,由AD是高,得出∠EAD的度数.
解答 解:∵∠BAC+∠B+∠C=180°,
∴∠BAC=180-∠B-∠C,
∵∠B=50°,∠C=60°,
∴∠BAC=70°,
∵AE是角平分线,
∴∠BAE=$\frac{1}{2}$∠BAC=35°,
∴∠AED=35°+50°=85°,
∵AD是高,
∴∠ADE=90°,
∴∠EAD=90°-85°=15°.
点评 本题考查了三角形的内角和定理,角平分线的定义,高的定义,以及外角的性质,三角形的外角等于和它不相邻的两个内角的和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.因为$\frac{3}{4}$a=1,所以( )
| A. | $\frac{3}{4}$是倒数 | B. | a是倒数 | C. | $\frac{3}{4}$和a都是倒数 | D. | $\frac{3}{4}$和a互为倒数 |
7.下列交换加数位置的变形中,正确的是( )
| A. | 1-4+5-4=1-4+4-5 | |
| B. | 4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 | |
| C. | 1-2+3-4=2-1+4-3 | |
| D. | -$\frac{1}{3}$+$\frac{3}{4}$-$\frac{1}{6}$-$\frac{1}{4}$=$\frac{1}{4}$+$\frac{3}{4}$-$\frac{1}{3}$-$\frac{1}{6}$ |
 如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图:
如图所示是由几个小立方块所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体的从正面看的图和从左面看的图: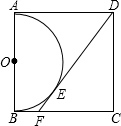 正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.
正方形ABCD的一边AB为直径在正方形内作半圆O,过点D作这个半圆的切线交BC于点F,E为切点,BF=1,求正方形ABCD的边长.