题目内容
7.在平面直角坐标系xOy中,图形W在坐标轴上的投影长度定义如下:设点P(x1,y1),Q(x2,y2)是图形W上的任意两点.若|x1-x2|的最大值为m,则图形W在x轴上的投影长度l1=M;若|y1-y2|的最大值为n,则图形W在y轴上的投影长度ly=n.如图1,图形W在x轴上的投影长度lx=|3-1|=2;在y轴上的投影长度ly=|4-0|=4.(1)已知点A(3,3),B(4,1).如图2所示,若图形W为△OAB,则lx4,ly3.
(2)已知点C(4,0),点D在直线y=2x+6上,若图形W为△OCD.当lx=ly时,求点D的坐标.
(3)若图形W为函数y=x2(a≤x≤b)的图象,其中0≤a<b.当该图形满足lx=ly≤1时,请直接写出a的取值范围.
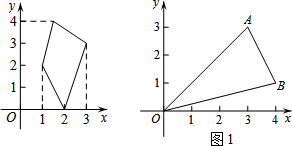
分析 (1)确定出点A在y轴的投影的坐标、点B在x轴上投影的坐标,于是可求得问题的答案;
(2)过点P作PD⊥x轴,垂足为P.设D(x,2x+6),则PD=|2x+6|.PC=|3-x|,然后依据lx=ly,列方程求解即可;
(3)设A(a,a2)、B(b,b2).分别求得图形在y轴和x轴上的投影,由lx=ly可得到b+a=1,然后根据0≤a<b可求得a的取值范围.
解答 解:(1)∵A(3,3),
∴点A在y轴上的正投影的坐标为(0,3).
∴△OAB在y轴上的投影长度ly=3.
∵B(4,1),
∴点B在x轴上的正投影的坐标为(4,0).
∴△OAB在x轴上的投影长度lx=4.
故答案为:4;3.
(2)如图1所示;过点P作PD⊥x轴,垂足为P.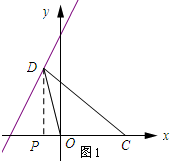
设D(x,2x+6),则PD=2x+6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4-x.
∵lx=ly,
∴2x+6=4-x,解得;x=-$\frac{2}{3}$.
∴D(-$\frac{2}{3}$,$\frac{14}{3}$).
如图2所示:过点D作DP⊥x轴,垂足为P.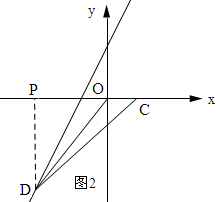
设D(x,2x+6),则PD=-2x-6.
∵PD⊥x轴,
∴P(x,0).
∴PC=4-x.
∵lx=ly,
∴-2x-6=4-x,解得;x=-10.
∴D(-10,-14).
综上所述,点D的坐标为(-$\frac{2}{3}$,$\frac{14}{3}$)或(-10,-14).
(3)如图3所示: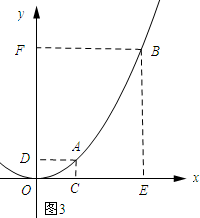
设A(a,a2)、B(b,b2).则CE=b-a,DF=b2-a2=(b+a)(b-a).
∵lx=ly,
∴(b+a)(b-a)=b-a,即(b+a-1)(b-a)=0.
∵b≠a,
∴b+a=1.
又∵0≤a<b,
∴a+a<1,
∴0≤a<$\frac{1}{2}$.
点评 本题主要考查的是二次函数的综合应用、解答本题主要应用了图形W在坐标轴上的投影长度定义、一次函数、二次函数图象上点的坐标与函数解析式的关系,依据lx=ly列出关于x的方程和不等式是解题的关键.

| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | -$\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
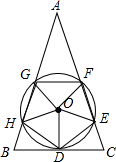 如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.
如图,五边形DEFGH是边长为2的正五边形,⊙O是正五边形DEFGH的外接圆,过点D作⊙D的切线,与GH、FE的延长线交分别于点B和C,延长HG、EF相交于点A,那么AB的长度是2+2$\sqrt{5}$.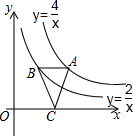 如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.
如图,点A在函数y=$\frac{4}{x}$(x>0)的图象上,过点A作AB∥x轴,交函数y=$\frac{2}{x}$(x>0)的图象于点B,点C在x轴上,连接AC、BC.则△ABC的面积是1.