题目内容
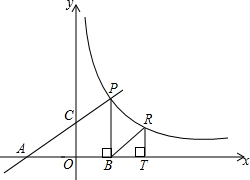 如图,直线y=
如图,直线y=| 1 |
| 2 |
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于点T,当△BRT与△AOC相似时,求点R的坐标.
考点:反比例函数综合题
专题:综合题
分析:(1)由一对公共角相等,一对直角相等,利用两对角相等的三角形相似即可得证;
(2)先求点A、C的坐标,根据点A、C分别在x、y轴上,设出A(a,0),C(0,c)代入直线的解析式可知;由△AOC∽△ABP,利用线段比求出BP,AB的值从而可求出点P的坐标即可;
(3)把P坐标代入求出反比例函数,设R点坐标为(x,y),根据△BRT与△AOC相似分两种情况,利用线段比联立方程组求出x,y的值,即可确定出R坐标.
(2)先求点A、C的坐标,根据点A、C分别在x、y轴上,设出A(a,0),C(0,c)代入直线的解析式可知;由△AOC∽△ABP,利用线段比求出BP,AB的值从而可求出点P的坐标即可;
(3)把P坐标代入求出反比例函数,设R点坐标为(x,y),根据△BRT与△AOC相似分两种情况,利用线段比联立方程组求出x,y的值,即可确定出R坐标.
解答:解:(1)∵∠CAO=∠PAB,∠AOC=∠ABP=90°,
∴△AOC∽△ABP;
(2)设A(a,0),C(0,c)由题意得
,
解得:
,
∴A(-4,0),C(0,2),即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP,
∴
=
,即
=
,
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,
∴AB=6,
∴P点坐标为(2,3);
(3)设反比例函数的解析式为y=
,
由题意得
=3,解得k=6,
∴反比例函数的解析式为y=
,
设R点的坐标为(x,y),
∵P点坐标为(2,3),
∴反比例函数解析式为y=
,
当△BTR∽△AOC时,
∴
=
,即
=
,
则有
,解得:
,
此时R的坐标为(
+1,
);
当△BRT∽△COA时,
∴
=
,即
=
,
解得:x1=3,x2=-1(不符合题意应舍去),
此时R坐标为(3,2),
综上,R的坐标为(
+1,
)或(3,2).
∴△AOC∽△ABP;
(2)设A(a,0),C(0,c)由题意得
|
解得:
|
∴A(-4,0),C(0,2),即AO=4,OC=2,
又∵S△ABP=9,
∴AB•BP=18,
又∵PB⊥x轴,
∴OC∥PB,
∴△AOC∽△ABP,
∴
| AO |
| AB |
| OC |
| BP |
| 4 |
| AB |
| 2 |
| BP |
∴2BP=AB,
∴2BP2=18,
∴BP2=9,
∴BP=3,
∴AB=6,
∴P点坐标为(2,3);
(3)设反比例函数的解析式为y=
| k |
| x |
由题意得
| k |
| 2 |
∴反比例函数的解析式为y=
| 6 |
| x |
设R点的坐标为(x,y),
∵P点坐标为(2,3),
∴反比例函数解析式为y=
| 6 |
| x |
当△BTR∽△AOC时,
∴
| AO |
| OC |
| BT |
| RT |
| 4 |
| 2 |
| x-2 |
| y |
则有
|
|
此时R的坐标为(
| 13 |
| ||
| 2 |
当△BRT∽△COA时,
∴
| AO |
| OC |
| RT |
| BT |
| 4 |
| 2 |
| y |
| x-2 |
解得:x1=3,x2=-1(不符合题意应舍去),
此时R坐标为(3,2),
综上,R的坐标为(
| 13 |
| ||
| 2 |
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法求函数解析式,相似三角形的判定与性质,一次函数与反比例函数的交点,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
相关题目
一个数的绝对值等于13,这个数是( )
| A、13 | ||
| B、-13 | ||
| C、±13 | ||
D、
|
对自然数列1,2,3,4,5,6…进行淘汰,淘汰的原则是:凡不能表示为两个合数之和的自然数均被淘汰,如:“1”应被淘汰;但12可以写成两个合数8与4的和,不应被淘汰.被保留下来的数按从小到大的顺序排列,则第2004个数是( )
| A、2015 | B、2014 |
| C、2013 | D、2012 |
下列各式中,属于同类二次根式的是( )
A、
| ||||||
B、
| ||||||
C、3a
| ||||||
D、
|
下列图案是由边长为单位长度的小正方形按一定规律排列而成,依此规律,第n个图中小正方形的个数为613个,则n的值为( )


| A、202 | B、204 |
| C、205 | D、207 |
 如图,已知第二象限内的点A在反比例函数y=
如图,已知第二象限内的点A在反比例函数y=