题目内容
已知：如图，AB=AC=24cm，AB的垂直平分线分别交AC、AB于D、E，△ABD的周长等于60cm，求DC的长．考点：线段垂直平分线的性质,等腰三角形的性质
专题：
分析：根据线段垂直平分线求出AD=BD，根据三角形的周长求出AD+DB=36，即可求出答案．
解答：解：
∵DE是AB的垂直平分线，
∴AD=BD，
∵C△ABD=AB+AD+DB=60，
∴AD+DB=60-24=36，
∴AD=18，
∴DC=AC-AD=24-18=6．
∵DE是AB的垂直平分线，
∴AD=BD，
∵C△ABD=AB+AD+DB=60，
∴AD+DB=60-24=36，
∴AD=18，
∴DC=AC-AD=24-18=6．
点评：本题考查了线段垂直平分线性质的应用，解此题的关键是求出AD=BD和求出AD+DB=36，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
相关题目
已知线段AB=8cm，在直线AB上有一点C，且BC=4cm，点M是线段AC的中点，则线段AM的长为（ ）
| A、2cm |
| B、4cm |
| C、2cm或6cm |
| D、4cm或6cm |
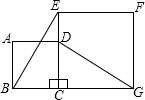如图所示，正方形ABCD的边CD在正方形ECGF的边CE上，连接BE，DG．（1）观察猜想线段BE与DG之间的大小关系，并证明你的结论；
（2）观察猜想直线BE与直线DG之间的位置关系，并证明你的结论．
有理数a、b在数轴上的位置如图所示，则下列各式中错误的是（ ）| A、b＜0＜a |
| B、|b|＞|a| |
| C、a+b＞0 |
| D、ab＜0 |
关于代数式a2-a+11的值叙述错误的是（ ）
| A、当a=0，1，2，3时，代数式的值为质数 |
| B、不能肯定a为任何自然数时，代数式的值都是质数 |
| C、当a=11时，代数式的值为合数 |
| D、当a为任意实数时，代数式的值不是质数就是合数 |
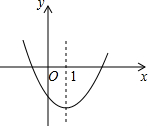二次函数y=ax2+bx+c图象如图，下列正确的个数为（ ）
如图，梯形ABCD沿上底AD方向向右平移到梯形EFGH，AD=4，BC=8，若阴影部分面积是四边形ABGH的