题目内容
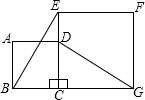 如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.
如图所示,正方形ABCD的边CD在正方形ECGF的边CE上,连接BE,DG.(1)观察猜想线段BE与DG之间的大小关系,并证明你的结论;
(2)观察猜想直线BE与直线DG之间的位置关系,并证明你的结论.
考点:全等三角形的判定与性质,正方形的性质
专题:
分析:(1)根据正方形的性质得出BC=CD,EC=GC,∠BCE=∠DCG=90°,根据SAS推出△BCE≌△DCG,根据全等三角形的性质得出即可;
(2)根据全等三角形的性质得出∠CBE=∠CDG,求出∠GBH+∠BGH=90°,推出∠BHG=90°即可.
(2)根据全等三角形的性质得出∠CBE=∠CDG,求出∠GBH+∠BGH=90°,推出∠BHG=90°即可.
解答:(1)猜想:BE=DG,
证明:∵在正方形ABCD中BC=CD,
在正方形ECGF中EC=GC,∠BCE=∠DCG=90°
在△BCE和△DCG中,
∴△BCE≌△DCG (SAS),
∴BE=DG;
(2)猜想:BE⊥DG,
证明:延长GD交BE于H点,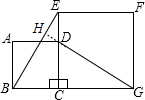
∵由(1)得△BCE≌△DCG,
∴∠CBE=∠CDG,
∵∠CDG+∠CGD=90°,
∴∠CBE+∠CGD=90°,
∴在△BHG中∠GBH+∠BGH=90°,
∴∠BHG=90°,
∴BE⊥DG.
证明:∵在正方形ABCD中BC=CD,
在正方形ECGF中EC=GC,∠BCE=∠DCG=90°
在△BCE和△DCG中,
|
∴△BCE≌△DCG (SAS),
∴BE=DG;
(2)猜想:BE⊥DG,
证明:延长GD交BE于H点,

∵由(1)得△BCE≌△DCG,
∴∠CBE=∠CDG,
∵∠CDG+∠CGD=90°,
∴∠CBE+∠CGD=90°,
∴在△BHG中∠GBH+∠BGH=90°,
∴∠BHG=90°,
∴BE⊥DG.
点评:本题考查了正方形的性质,全等三角形的性质和判定的应用,解此题的关键是求出△BCE≌△DCG,全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
 已知线段AB=6厘米,延长AB到点C,使得BC=
已知线段AB=6厘米,延长AB到点C,使得BC=
 已知:如图,AB=AC=24cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于60cm,求DC的长.
已知:如图,AB=AC=24cm,AB的垂直平分线分别交AC、AB于D、E,△ABD的周长等于60cm,求DC的长. 如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标.
如图,OA=10,OB=6,∠xOA=60°,∠xOB=135°,求A,B两点坐标. 如图,△ABC中,AB、BC、CA的中点分别是E,F,G,AD是高.则下列选项正确的有( )个
如图,△ABC中,AB、BC、CA的中点分别是E,F,G,AD是高.则下列选项正确的有( )个