题目内容
9.在Rt△ABC中,∠ACB=90°,cosB=$\frac{2}{3}$,把这个直角三角形绕顶点C旋转后得到Rt△FEC,其中点E正好落在AB上,EF与AC相交于点D,那么$\frac{AE}{EB}$=$\frac{9\sqrt{5}-20}{4}$,$\frac{AD}{FD}$=$\frac{9\sqrt{5}-20}{3}$.分析 过C作CG⊥AB于G,根据已知条件设BC=2,AB=3,由勾股定理得AC=$\sqrt{5}$,由射影定理得CB2=BG•AB,得到BG=$\frac{4}{3}$,由旋转的性质得CE=BC=2,FC═AC=$\sqrt{5}$,∠F=∠A,根据勾股定理得到EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=$\sqrt{{2}^{2}-(\frac{4}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$,根据根于是矩形的性质得到BE=$\frac{4\sqrt{5}}{4}$,根据相似三角形的性质即可得到结论.
解答 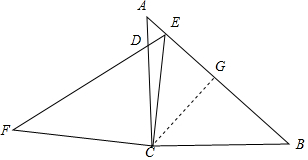 解:过C作CG⊥AB于G,
解:过C作CG⊥AB于G,
∵cosB=$\frac{2}{3}$,
设BC=2,AB=3,由勾股定理得AC=$\sqrt{5}$,
由射影定理得CB2=BG•AB,
∴BG=$\frac{4}{3}$,
由旋转的性质得CE=BC=2,FC═AC=$\sqrt{5}$,
∠F=∠A,
∴EG=$\sqrt{C{E}^{2}-C{G}^{2}}$=$\sqrt{{2}^{2}-(\frac{4}{3})^{2}}$=$\frac{2\sqrt{5}}{3}$,BG=EG,
∴BE=$\frac{4\sqrt{5}}{4}$,
∴AE=3-$\frac{4\sqrt{5}}{3}$,$\frac{AE}{EB}$=$\frac{3-\frac{4\sqrt{5}}{3}}{\frac{4\sqrt{5}}{3}}$=$\frac{9\sqrt{5}-20}{4}$,
∵∠FDC=∠ADE,
∴△ADF∽△FDC,
∴$\frac{AD}{FD}$=$\frac{AE}{CF}$=$\frac{3-\frac{4\sqrt{5}}{3}}{\sqrt{5}}$=$\frac{9\sqrt{5}-20}{3}$,
故答案为:$\frac{9\sqrt{5}-20}{4}$,$\frac{9\sqrt{5}-20}{3}$.
点评 该题主要考查了旋转变换的性质、勾股定理、相似三角形的判定等几何知识点及其应用问题;解题的方法是作辅助线,将分散的条件集中;解题的关键是灵活运用旋转变换的性质、勾股定理等几何知识点来分析、判断、推理或解答.

| A. | 14 | B. | 10 | C. | 3 | D. | 2 |
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
(2)前8场比赛结束时,某队是否存在胜场总积分等于它的负场总积分的情况?为什么?
(3)8场比赛以后还剩余m场比赛,当比赛结束时,该队是否存在胜场总积分等于它的负场总积分的情况?如果存在,求出胜场场次;如果不存在,请说明理由.
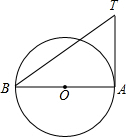 如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=50°.
如图,AT切⊙O于点A,AB是⊙O的直径.若∠ABT=40°,则∠ATB=50°.
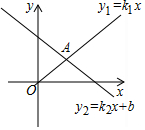 如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1<y2.(填“>”或“<”).
如图,正比例函数y1=k1x和一次函数y2=k2x+b的图象相交于点A(2,1),当x<2时,y1<y2.(填“>”或“<”).