题目内容
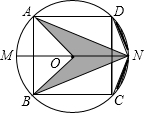 如图所示,正方形ABCD内接于⊙O,直径MN∥AD,则阴影部分面积占圆面积的
如图所示,正方形ABCD内接于⊙O,直径MN∥AD,则阴影部分面积占圆面积的考点:扇形面积的计算
专题:计算题
分析:连结OC、OD,如图,设⊙O的半径为r,利用正方形的性质得MN∥BC,根据三角形面积公式得S△DON=S△AON,S△CON=S△BON,于是利用面积的和差得到S阴影部分=S扇形COD,再利用正方形的性质得∠COD=90°,则根据扇形面积公式可计算出S扇形COD=
πr2,所以阴影部分面积占圆面积的
.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解: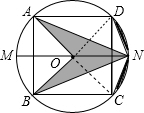 连结OC、OD,如图,设⊙O的半径为r,
连结OC、OD,如图,设⊙O的半径为r,
∵直径MN∥AD,
而AD∥BC,
∴MN∥BC,
∴S△DON=S△AON,S△CON=S△BON,
∴S阴影部分=S扇形COD,
∵四边形ABCD为正方形,
∴∠COD=90°,
∴S扇形COD=
=
πr2,
而⊙O的面积为πr2,
∴阴影部分面积占圆面积的
.
故答案为
.
 连结OC、OD,如图,设⊙O的半径为r,
连结OC、OD,如图,设⊙O的半径为r,∵直径MN∥AD,
而AD∥BC,
∴MN∥BC,
∴S△DON=S△AON,S△CON=S△BON,
∴S阴影部分=S扇形COD,
∵四边形ABCD为正方形,
∴∠COD=90°,
∴S扇形COD=
| 90•π•r2 |
| 360 |
| 1 |
| 4 |
而⊙O的面积为πr2,
∴阴影部分面积占圆面积的
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评:本题考查了扇形面积的计算:设圆心角是n°,圆的半径为R的扇形面积为S,则S扇形=
πR2或S扇形=
lR(其中l为扇形的弧长.也考查了正方形的性质和利用面积的和差计算不规则图形的面积.
| 360 |
| n |
| 1 |
| 2 |

练习册系列答案
 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
下列四个角中最有可能和68°角互补的角是( )
A、 |
B、 |
C、 |
D、 |
 如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )
如图,AB=12,C为AB的中点,点D在线段AC上,且AD:CB=1:3,则DB的长度为( )| A、4 | B、6 | C、8 | D、10 |
已知不等式-x+5>3x-3的解集是2<x,则直线y=-x+5与y=3x-3的交点坐标是( )
| A、(2,3) |
| B、(3,2) |
| C、(3,-2) |
| D、(-3,2) |

 如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,将线段AB绕点B顺时针旋转90°.将线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均落在格点上,将线段AB绕点B顺时针旋转90°.将线段A′B,点A的对应点为A′,连接AA′交线段BC于点D.