题目内容
如图1,AB是⊙O的直径,点E是弧AD上的一点,∠DBC=∠BED.
(1)求证:BC是⊙O的切线;
(2)若AD=6,CD=2.
①求BD的长;
②如图2所示,请求出阴影部分的面积.

(1)求证:BC是⊙O的切线;
(2)若AD=6,CD=2.
①求BD的长;
②如图2所示,请求出阴影部分的面积.

考点:切线的判定,扇形面积的计算
专题:证明题
分析:(1)根据圆周角定理得∠ADB=90°,则∠A+∠ABD=90°,加上∠BED=∠A,∠DBC=∠BED,易得∠ABC=90°,于是根据切线的判定定理可得BC是⊙O的切线;
(2)①证明△BDC∽△ADB,利用相似比可计算出BD=2
;
②连结OD,作DH⊥AB于H,如图2,先根据勾股定理计算出AB=4
,则OB=OD=2
,于是可判断△OBD为等边三角形,则∠BOD=60°,然后根据含30度的直角三角形三边的关系求出DH=
OH=3,然后根据扇形面积公式和三角形面积公式,利用阴影部分的面积=S△OBD+S△BDC-S扇形OBD进行计算即可.
(2)①证明△BDC∽△ADB,利用相似比可计算出BD=2
| 3 |
②连结OD,作DH⊥AB于H,如图2,先根据勾股定理计算出AB=4
| 3 |
| 3 |
| 3 |
解答: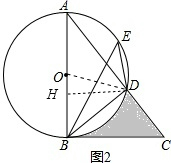 (1)证明:∵AB是⊙O的直径,
(1)证明:∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠BED=∠A,∠DBC=∠BED,
∴∠DBC+∠ABD=90°,即∠ABC=90°,
∴AB⊥BC,
∴BC是⊙O的切线;
(2)解:①∵∠DBC=∠A,∠BDC=∠BDA=90°,
∴△BDC∽△ADB,
∴
=
,即
=
,
∴BD=2
;
②连结OD,作DH⊥AB于H,如图2,
在Rt△ABD中,∵AD=6,BD=2
,
∴AB=
=4
,
∴OB=OD=2
,
∴△OBD为等边三角形,
∴∠BOD=60°,
∴∠ODH=30°,
∴OH=
OD=
,
∴DH=
OH=3,
∴阴影部分的面积=S△OBD+S△BDC-S扇形OBD
=
×2
×3+
×2
×2-
=5
-2π.
 (1)证明:∵AB是⊙O的直径,
(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵∠BED=∠A,∠DBC=∠BED,
∴∠DBC+∠ABD=90°,即∠ABC=90°,
∴AB⊥BC,
∴BC是⊙O的切线;
(2)解:①∵∠DBC=∠A,∠BDC=∠BDA=90°,
∴△BDC∽△ADB,
∴
| BD |
| AD |
| CD |
| BD |
| BD |
| 6 |
| 2 |
| BD |
∴BD=2
| 3 |
②连结OD,作DH⊥AB于H,如图2,
在Rt△ABD中,∵AD=6,BD=2
| 3 |
∴AB=
| AD2+BD2 |
| 3 |
∴OB=OD=2
| 3 |
∴△OBD为等边三角形,
∴∠BOD=60°,
∴∠ODH=30°,
∴OH=
| 1 |
| 2 |
| 3 |
∴DH=
| 3 |
∴阴影部分的面积=S△OBD+S△BDC-S扇形OBD
=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
60•π•(2
| ||
| 360 |
=5
| 3 |
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了圆周角定理、相似三角形的判定与性质和扇形的面积公式.

练习册系列答案
相关题目
深圳是一个美丽的海滨城市,海岸线长约230000米,东临大亚湾,西濒珠江口,数据230000用科学记数法表示为( )
| A、23×104 |
| B、2.3×105 |
| C、2.3×106 |
| D、0.23×107 |
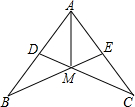 如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )
如图,AB=AC,AD=AE,∠BAC=60°,∠C=25°,则∠BMD的度数为( )| A、50° | B、65° |
| C、70° | D、85° |
 如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF⊥DE于F,求证:CF平分∠DCE.
如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC,CF⊥DE于F,求证:CF平分∠DCE.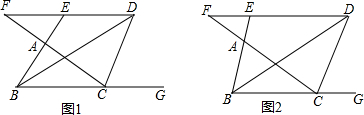
 如图,等边△ABC内接于⊙O,P是
如图,等边△ABC内接于⊙O,P是
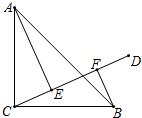 如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由.
如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由. 如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是
如图,△ABT是等腰直角三角形,AB是⊙O的直径,且AB=4,则图中阴影部分的面积是