题目内容
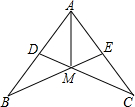如图，AB=AC，AD=AE，∠BAC=60°，∠C=25°，则∠BMD的度数为（ ）| A、50° | B、65° |
| C、70° | D、85° |
考点：全等三角形的判定与性质
专题：
分析：首先根据三角形外角的性质可得∠BDC=25°+60°=85°，然后再证明△AEB≌△ADC，根据全等三角形的性质可得∠B=∠C=25°，再利用三角形内角和定理计算出∠BMD的度数．
解答：证明：∵∠BAC=60°，∠C=25°，
∴∠BDC=25°+60°=85°，
在△AEB和△ADC中，
，
∴△AEB≌△ADC（SAS），
∴∠B=∠C=25°，
∴∠DNB=180°-25°-85°=70°，
故选：C．
∴∠BDC=25°+60°=85°，
在△AEB和△ADC中，
|
∴△AEB≌△ADC（SAS），
∴∠B=∠C=25°，
∴∠DNB=180°-25°-85°=70°，
故选：C．
点评：此题主要考查了全等三角形的判定和性质，以及三角形外角的性质，关键是正确证明△AEB≌△ADC．
练习册系列答案
相关题目
各边长均为整数、周长为10的三角形有（ ）
| A、1个 | B、2个 | C、3个 | D、4个 |
将数8200000用科学记数法表示为（ ）
| A、8.2×107 |
| B、82×105 |
| C、8.2×106 |
| D、0.82×107 |
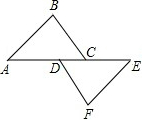如图，点A、D、C、E在同一条直线上，AB∥EF，AB=EF，∠B=∠F，AE=10，AC=7，则CD的长为（ ）| A、5.5 | B、4 | C、4.5 | D、3 |
如图，在△ABC中，AB=AC，∠A=90°，点D在线段BC上，∠BDE=
如图矩形ABCD中，AB=6，BC=8，若将矩形折叠，使B点与D点重合，求折痕EF的长．