题目内容
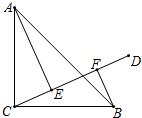 如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由.
如图,在△ABC中,∠ABC=90°,AC=BC,AE⊥CD,BF⊥CD,垂足分别为点E,F,图中BF与哪条线段相等?说明理由.考点:全等三角形的判定与性质
专题:
分析:利用AE⊥CD,BF⊥CD,得出∠BFC=∠CEA,进一步利用已知条件得出∠BCF=∠CAE,证得△ACE≌△CBF,得出BF=CE.
解答:解:BF=CE.
理由如下:
∵AE⊥CD,BF⊥CD,
∴∠BFC=∠CEA,
∵∠ACE+∠BCF=∠ACE+∠CAE=90°,
∴∠BCF=∠CAE,
在△ACE和△CBF中,
∴△ACE≌△CBF (ASA)
∴BF=CE.
理由如下:
∵AE⊥CD,BF⊥CD,
∴∠BFC=∠CEA,
∵∠ACE+∠BCF=∠ACE+∠CAE=90°,
∴∠BCF=∠CAE,
在△ACE和△CBF中,
|
∴△ACE≌△CBF (ASA)
∴BF=CE.
点评:此题考查三角形全等的判定与性质,灵活运用题目中的条件,找出边角关系,证得三角形全等是关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目

 如图,在△ABC中,AB=AC,∠A=90°,点D在线段BC上,∠BDE=
如图,在△ABC中,AB=AC,∠A=90°,点D在线段BC上,∠BDE= 如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长.
如图矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,求折痕EF的长. 已知直角三角形ABC的内切圆与三条边分别切于点D、E、F,若AC=3cm,BC=4cm,求内切圆半径的大小.
已知直角三角形ABC的内切圆与三条边分别切于点D、E、F,若AC=3cm,BC=4cm,求内切圆半径的大小. 如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=2∠AOB
如图所示,直线AE上有一点O,∠AOB=30°,∠BOC=2∠AOB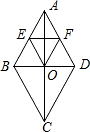 如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,
如图,菱形ABCD的对角线AC与BD相交于点O,点E,F分别为边AB,AD的中点,连接EF,OE,OF,