题目内容
2．（1）分解因式：6xy2-12x2y3（2）分式计算：$\frac{x-5}{4-x}$-1-$\frac{1}{x-4}$．
分析 （1）根据提公因式法，可得答案；
（2）根据通分，可得同分母分式，根据同分母分式的加减，可得答案．
解答 解：（1）原式=6xy2（1-2xy）；
（2）原式=$\frac{5-x}{x-4}$-$\frac{x-4}{x-4}$-$\frac{1}{x-4}$=$\frac{5-x-x+4-1}{x-4}$=$\frac{2（4-x）}{x-4}$=-2．
点评 本题考查了分式的加减，通分化成同分母分式的加减是解题关键．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
13．下列各式的分解因式中，没有用到公式法的是（ ）
| A． | 3m2-6mn+3n2=3（m-n）2 | B． | x2b+ab2+ab=ab（a+b+1） | ||
| C． | mx2-4m=m（x-2）（x+2） | D． | x2+12x+36=（x+6）2 |
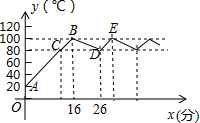张老师办公室的饮水机具有自动调节功能，开机后自动进行加热状态，水温y（℃）与开机后用时x（分钟）成一次函数关系，当水温上升到100℃时停止加热，水温开始下降，此时水温y（℃）与开机后用时x（分钟）仍成一次函数某天早晨7：00时，张老师打开饮水机，水温变化情况如图所示．
14．已知$\frac{a}{b+c+d}$=$\frac{b}{a+c+d}$=$\frac{c}{a+b+d}$=$\frac{d}{a+b+c}$=k，则k的值为（ ）
| A． | -1 | B． | 3 | C． | -1或$\frac{1}{3}$ | D． | 4 |
问题：