题目内容
3.已知三个有理数abc≠0,且a+b+c=0,当y=$\frac{|a|}{a}$+$\frac{b}{|b|}$+$\frac{|c|}{c}$+$\frac{abc}{|abc|}$时,(1)求出y的值.
(2)先化简4xy2-3x2y-{3x2y+xy2-[2xy2-4x2y+(x2y-2xy2)]},再把(1)中y的值代入求值.
分析 (1)分类讨论:a>0,b>0,c<0时,a>0,b<0,c<0,根据绝对值的意义,可化简绝对值,根据有理数的运算,可得答案;
(2)根据去括号、合并同类项,可化简整式,根据代数式求值,可得答案.
解答 解:(1)当a>0,b>0,c<0时,y=1+1-1-1=0,
当a>0,b<0,c<0时,y=1-1-1+1=0,
(2)原式=4xy2-3xy2-{3x2y+xy2-[2xy2-4xy2+x2y-2xy2]}
=4xy2-3xy2-{3x2y+xy2-2xy2+4xy2-x2y+2xy2}
=4xy2-3xy2-3x2y-xy2+2xy2-4xy2+x2y-2xy2
=3xy2-9x2y
当y=0时,原式=0.
点评 本题考查了整式的化简求值,分类讨论是解题关键,以防遗漏;去括号是解题关键,先去小括号,再去中括号,最后去大括号.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
13.直线y=x-3向上平移m个单位后与y=2x+4的交点在第二象限,则m的取值范围为( )
| A. | 5<m<7 | B. | 3<m<4 | C. | m>7 | D. | m<4 |
14.已知|x|=4,|y|=5,且xy<0,则x+y的值等于( )
| A. | 9或-9 | B. | 9或-1 | C. | 1或-1 | D. | -9或-1 |
13. 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
 如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )
如图,△ABC内接于⊙O,BD是⊙O的直径.若∠DBC=33°,则∠A等于( )| A. | 33° | B. | 57° | C. | 67° | D. | 66° |
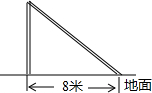 如图,台风过后,一颗白杨树在高地某处断裂,白杨树的顶部落在离白杨树根部8米处,已知白杨树高16米,你能求出白杨树在离根部多少米的位置断裂吗?
如图,台风过后,一颗白杨树在高地某处断裂,白杨树的顶部落在离白杨树根部8米处,已知白杨树高16米,你能求出白杨树在离根部多少米的位置断裂吗? 如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
如图,已知数轴上点A表示的数为6,B是你数轴上一点,且AB=10,动点P从点O出发,以每秒6个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.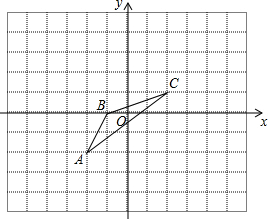 如图,在平面直角坐标系中,
如图,在平面直角坐标系中, 已知一块长方形绿地,在它的中央布置一个长方形花坛,四周铺上草地.设计的条件是这样的:绿地的长要比宽大4米,花坛四周的草地的宽都是2米,草地的总面积是80m2.求划出的这块长方形绿地的长和宽应当各是多少米?
已知一块长方形绿地,在它的中央布置一个长方形花坛,四周铺上草地.设计的条件是这样的:绿地的长要比宽大4米,花坛四周的草地的宽都是2米,草地的总面积是80m2.求划出的这块长方形绿地的长和宽应当各是多少米?