题目内容
7．
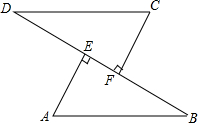如图，已知AB=CD，AE⊥BD，CF⊥BD，垂足分别为E，F，BF=DE，求证：AB∥CD．
分析 根据全等三角形的判定与性质，可得∠B=∠D，根据平行线的判定，可得答案．
解答 证明：∵AE⊥BD，CF⊥BD，
∴∠AEB=∠CFD=90°，
∵BF=DE，
∴BF+EF=DE+EF，
∴BE=DF．
在Rt△AFB和Rt△CFD中，
$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\end{array}\right.$，
∴Rt△AFB≌Rt△CFD（HL），
∴∠B=∠D，
∴AB∥CD．
点评 本题考查了全等三角形的判定与性质，利用等式的性质得出BE=DF是解题关键，又利用了全等三角形的判定与性质．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
3．某校组织“大手拉小手，义卖献爱心”活动，购买了黑白两种颜色的文化衫共140件，进行手绘设计后了出售，所获利润全部捐给山区困难孩子．每件文化衫的批发价和零售价如下表：
假设文化衫全部售出，共获利1860元，求黑白两种文化衫各多少件？
| 批发价（元） | 零售价（元） | |
| 黑色文化衫 | 10 | 25 |
| 白色文化衫 | 8 | 20 |
