题目内容
10.在平面直角坐标系中,直线y=-$\frac{3}{4}$x+6分别与x轴、y轴交于点A,B.当点P在线段AB(点P不与A,B重合)上运动时,在坐标系内存在一点N,使得以O,B,P,N为顶点的四边形为菱形.请直接写出N点坐标(-4,3),($\frac{144}{25}$,$\frac{192}{25}$),($\frac{24}{5}$,-$\frac{18}{5}$).分析 分三种情况讨论:以OB为菱形OPBN的对角线,以PB为菱形OPBN的对角线,以OP为菱形BPNO的对角线,分别根据菱形的性质以及一次函数图象上点的坐标特征进行计算,即可得到N点坐标.
解答 解:∵直线y=-$\frac{3}{4}$x+6分别与x轴、y轴交于点A,B,
∴A(8,0),B(0,6).
分三种情况:
①如图所示,以OB为菱形OPBN的对角线,点P与点N关于OB对称,
由BP=OP可得,∠PBO=∠POB,
根据∠PBO+∠PAO=∠POB+∠POA=90°,可得∠POA=∠PAO,
∴PO=PA,
∴P是AB的中点,即P(4,3),
∴N(-4,3);
②如图所示,以PB为菱形OPBN的对角线,设P(n,-$\frac{3}{4}$n+6),
∵四边形OPNB为菱形,B(0,6),
∴OP=OB=6=$\sqrt{{n}^{2}+(-\frac{3}{4}n+6)^{2}}$,
解得:n=$\frac{144}{25}$或n=0(舍去),
∴点P($\frac{144}{25}$,$\frac{42}{25}$),
∴点N($\frac{144}{25}$,6+$\frac{42}{25}$),即N($\frac{144}{25}$,$\frac{192}{25}$);
③如图所示,以OP为菱形BPNO的对角线,设P(m,-$\frac{3}{4}$m+6)
∵四边形ONPB为菱形,B(0,6),
∴BP=OB=6=$\sqrt{{m}^{2}+(-\frac{3}{4}m+6-6)^{2}}$,
解得m=$\frac{24}{5}$,
∴P($\frac{24}{5}$,$\frac{12}{5}$),
∴N($\frac{24}{5}$,$\frac{12}{5}$-6),即N($\frac{24}{5}$,-$\frac{18}{5}$),
综上所述,N点坐标为(-4,3),($\frac{144}{25}$,$\frac{192}{25}$),($\frac{24}{5}$,-$\frac{18}{5}$).
故答案为:(-4,3),($\frac{144}{25}$,$\frac{192}{25}$),($\frac{24}{5}$,-$\frac{18}{5}$).
点评 本题主要考查了一次函数图象上点的坐标特征以及菱形的判定的运用,解决问题的关键是依据题意画出图形,进行分类讨论.解题时注意菱形的四条边都相等.

 一线名师提优试卷系列答案
一线名师提优试卷系列答案| A. | -121 | B. | -100 | C. | 100 | D. | 121 |
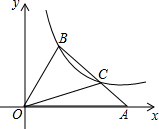 如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴上的正半轴上,BC=2AC,点B、C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积为6.
如图,在平面直角坐标系xOy中,△OAB的顶点A在x轴上的正半轴上,BC=2AC,点B、C在反比例函数y=$\frac{3}{x}$(x>0)的图象上,则△OAB的面积为6. 如图,折叠一张长方形纸片,已知∠1=66°,则∠2的度数是57°.
如图,折叠一张长方形纸片,已知∠1=66°,则∠2的度数是57°.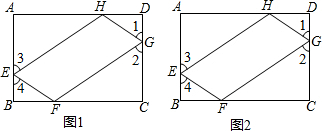
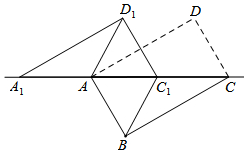 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1,若∠ACB=30°,AB=1,CC1=x(0<x<2),△ACD与△A1C1D1重叠部分的面积为S,则下列结论: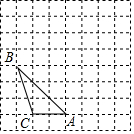 如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题:
如图,方格纸中每一个小方格的边长为1个单位,试解答下列问题: