题目内容
1.常温下,有一种烧水壶加热1.5升的纯净水时,加热中的水温y(℃)与加热时间x(秒)之间近似地满足一次函数关系.经实验可知,在常温下用这种壶将1.5升的纯净水加热到70℃时,所用时间为3分16秒;再加热40秒,水温正好达到80℃.(1)求出y与x之间的函数关系式;
(2)在常温下,若用这种烧水壶将1.5升的28℃纯净水烧开(温度为100℃),则加热多长时间?
分析 (1)利用待定系数法即可直接求得函数解析式;
(2)在(1)求得的解析式中,求得当温度是100℃和28℃时对应的时间,求两者的差即可.
解答 解:(1)3分16秒=196秒,196+40=236秒,
设y与x的函数关系式是y=kx+b,则$\left\{\begin{array}{l}{196\\;k+\\;b=70}\\{236\\;k+\\;b=80}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{\\;k=\frac{1}{4}}\\{\\;b=21}\end{array}\right.$,
则函数的解析式是y=$\frac{1}{4}$x+21;
(2)在y=$\frac{1}{4}$x+21中,令y=100,则$\frac{1}{4}$x+21=100,
解得:x=316,
在y=$\frac{1}{4}$x+21中,令y=28,则$\frac{1}{4}$x+21=28,解得:x=28,
则用这种烧水壶将1.5升的28℃纯净水烧开(温度为100℃),则加热时间是316-28=288(秒).
答:加热时间是288秒.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意时间单位要统一是本题的关键.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
9.如果一个多边形的对角线的条数是边数的一半,那么这个多边形是( )
| A. | 三角形 | B. | 四边形 | C. | 五边形 | D. | 六边形 |
19.下列图形中不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
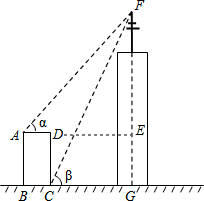 如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
如图,某高楼顶部有一信号发射塔,在矩形建筑物ABCD的A,C两点测得该塔顶端F的仰角分别为和β,矩形建筑物宽度AD=20m,高度DC=33m.求:
