题目内容

5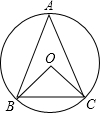．如图所示，△ABC内接于⊙O，AB=AC，∠BOC=120°．求$\widehat{AB}$和$\widehat{AC}$的度数．

分析 根据圆周角定理求出∠A的度数，根据弧、弦的关系得到$\widehat{AB}$=$\widehat{AC}$，根据三角形内角和定理计算即可．

解答 解：由圆周角定理得，∠A=$\frac{1}{2}$∠BOC=60°，
∵AB=AC，
∴∠ABC=∠ACB=60°，$\widehat{AB}$=$\widehat{AC}$，
∴$\widehat{AB}$和$\widehat{AC}$的度数都是120°．

点评 本题考查的是三角形的外接圆和外心的概念，掌握圆周角定理、等腰三角形的性质是解题的关键．

练习册系列答案
相关题目
15．已知三角形两边的长分别是4和10，则此三角形第三边的长不可能是（　　）
A．6B．7C．9.5D．10
16．如果把分式$\frac{x-y}{x+y}$中的和都扩大了3倍，那么分式的值（　　）
A．扩大3倍B．缩小6倍C．缩小3倍D．不变
13．下列函数中，y是x的二次函数的是（　　）
A．y=2x-1B．y=-$\frac{1}{x}$C．y=x-x2D．y=$\frac{1}{{x}^{2}}$+x
20．若关于x的一元二次方程（k-1）x2+4x+1=0有两个不相等的实数根，则k的取值范围是（　　）
A．k＜5B．k＞5C．k≤5，且k≠1D．k＜5，且k≠1
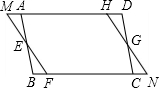10．如图四边形ABCD、MFNH都是平行四边形，MAHD和BFCN都在一直线上，HD=FB．
求证：（1）MA=CN；（2）∠AEM=∠CGN．
17．使分式$\frac{x}{x-1}$有意义的x的取值范围是（　　）
A．x≠1B．x≠0C．x≠-1D．x≠0且x≠1．
14．观察下列各式，发现规律：$\sqrt{1+\frac{1}{3}}$=2$\sqrt{\frac{1}{3}}$；$\sqrt{2+\frac{1}{4}}$=3$\sqrt{\frac{1}{4}}$；$\sqrt{3+\frac{1}{5}}$=4$\sqrt{\frac{1}{5}}$；…
（1）填空：$\sqrt{4+\frac{1}{6}}$=5$\sqrt{\frac{1}{6}}$，$\sqrt{5+\frac{1}{7}}$=6$\sqrt{\frac{1}{7}}$；
（2）计算（写出计算过程）：$\sqrt{2015+\frac{1}{2017}}$；
（3）请用含自然数n（n≥1）的代数式把你所发现的规律表示出来．
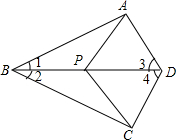13．如图，已知∠1=∠2，∠3=∠4，点P是BC上任意一点，求证：PA=PC．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网