题目内容
1. 如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )
如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )①∠ACB=2∠BDE;②∠AEB=90°;③AC=BD;④AC⊥BD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据折叠的性质得到∠BDE=∠BCE,根据全等三角形的性质得到∠BCE=∠ACE,于是得到∠ACB=2∠BDE;故①正确;根据全等三角形的性质得到AC=BC,等量代换得到AC=BD,故③正确;根据已知条件得到直线CE垂直平分AB,得到点E在AB的垂直平分线上,且点E是等边△ABC内一点,求得60°<∠AEB<180°,故②错误,根据三角形的内角和得到60°<∠AGB<180°,故④错误.
解答 解:∵将△BCE沿着BE折叠得到△BDE,
∴∠BDE=∠BCE,
在△BCE与△ACE中,$\left\{\begin{array}{l}{BC=AC}\\{AE=BE}\\{CE=CE}\end{array}\right.$,
∴△BCE≌△ACE,
∴∠BCE=∠ACE,
∴∠ACB=2∠BCE,
∴∠ACB=2∠BDE;故①正确;
∵△BCE≌△ACE,
∴AC=BC,
∵BC=BD,
∴AC=BD,故③正确;
∵AC=BC,AE=BE,
∴直线CE垂直平分AB,
∴点E在AB的垂直平分线上,且点E是等边△ABC内一点,
∴60°<∠AEB<180°,故②错误,
设AC,BD交于G,
∵∠EBD=∠EAC,∠AFG=∠BFE,
∴∠AGF=∠BEF,
∵60°<∠AEB<180°,
∴60°<∠AGB<180°,故④错误.
故选B.
点评 本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
相关题目
6.与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{9}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{3}}$ |
 如图,已知O为△ABC内一点,D,E,F分别是OA,OB,OC的中点.
如图,已知O为△ABC内一点,D,E,F分别是OA,OB,OC的中点.
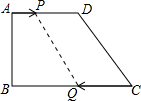 直角梯形ABCD中,∠B=90°,AD∥BC,AD=18cm,BC=21cm,点P从点A以1cm/s的速度向点D运动,同时点Q从点C以2cm/s的速度向点B运动.问:
直角梯形ABCD中,∠B=90°,AD∥BC,AD=18cm,BC=21cm,点P从点A以1cm/s的速度向点D运动,同时点Q从点C以2cm/s的速度向点B运动.问: