题目内容
12.解方程:(1)(2y+1)2-8(2y+1)+16=0;
(2)9x2-12x+4=(3-2x)2.
分析 (1)先设2y+1=t,则方程即可变形为t2-8t+16=0,解方程即可求得t即(2y+1)的值.
(2)先将原方程的左边转化为完全平方的形式,然后利用换元法解方程.
解答 解:(1)设2y+1=t.则由原方程,得
t2-8t+16=0,
∴(t-4)2=0,
∴t-4=0,
解得t=4;
∴2y+1=4,
故y1=y2=1.5.
(2)原方程变形为(3x-2)2=(3-2x)2,
两边直接开平方得:3x-2=3-2x,或3x-2=2x-3,
解得:x=1或x=-1.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.本题利用了换元法解方程.

练习册系列答案
相关题目
17.下列运算中,正确的是( )
| A. | 22×23=26 | B. | 22×23=46 | C. | 22×23=25 | D. | 22×23=45 |
1. 如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )
如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )
①∠ACB=2∠BDE;②∠AEB=90°;③AC=BD;④AC⊥BD.
 如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )
如图,点E是等边△ABC内一点,连按BE、AE,且AE=BE,将线段BC沿BE翻折,使点C落在点D处,连接DE.下列结论正确的个数为( )①∠ACB=2∠BDE;②∠AEB=90°;③AC=BD;④AC⊥BD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2. 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,则下列结论错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,则下列结论错误的是( )
 如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,则下列结论错误的是( )
如图,在△ABC中,点D、E分别在AB、AC上,且DE∥BC,则下列结论错误的是( )| A. | $\frac{BD}{AB}=\frac{EC}{AC}$ | B. | $\frac{AD}{DB}=\frac{AE}{EC}$ | C. | $\frac{AD}{AB}=\frac{AE}{AC}$ | D. | $\frac{AD}{DB}=\frac{DE}{BC}$ |
 如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),D(2,7),连接AD交y轴于C点.
如图,在平面直角坐标系中,已知点A(-5,0),B(5,0),D(2,7),连接AD交y轴于C点.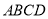 中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)
中,横向阴影部分是矩形,另一阴影部分是平行四边形.依照图中标注的数据,计算图中空白部分的面积,已知a=2b=6c,其面积是_________________________.(用含c的代数式表示)