题目内容
12.将$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{8}}{8}$按从小大的顺序排列$\frac{\sqrt{8}}{8}$<$\frac{\sqrt{7}}{7}$<$\frac{\sqrt{6}}{6}$.分析 首先将$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{8}}{8}$都化成以1为分子的分数,然后根据分子相同,分母越小,则分数越大,将$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{8}}{8}$按从小大的顺序排列即可.
解答 解:$\frac{\sqrt{6}}{6}$=$\frac{1}{\sqrt{6}}$,$\frac{\sqrt{7}}{7}$=$\frac{1}{\sqrt{7}}$,$\frac{\sqrt{8}}{8}$=$\frac{1}{\sqrt{8}}$,
∵$\frac{1}{\sqrt{8}}<\frac{1}{\sqrt{7}}<\frac{1}{\sqrt{6}}$,
∴将$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{8}}{8}$按从小大的顺序排列$\frac{\sqrt{8}}{8}$<$\frac{\sqrt{7}}{7}$<$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{\sqrt{8}}{8}$<$\frac{\sqrt{7}}{7}$<$\frac{\sqrt{6}}{6}$.
点评 (1)此题主要考查了实数大小比较的方法,要熟练掌握,解答此题的关键是要明确:正实数>0>负实数,两个负实数绝对值大的反而小.
(2)解答此题的关键是将$\frac{\sqrt{6}}{6}$,$\frac{\sqrt{7}}{7}$,$\frac{\sqrt{8}}{8}$都化成以1为分子的分数.

练习册系列答案
相关题目
3.已知等边三角形的高为3,则边长为( )
| A. | 1.5 | B. | 2$\sqrt{3}$ | C. | 6 | D. | $\sqrt{3}$ |
20.下列函数中,属于二次函数的是( )
| A. | $y=\sqrt{{x^2}+1}$ | B. | y=ax2+bx+c | C. | $y=\frac{{{x^2}+1}}{x}$ | D. | $y=-\frac{1}{2}(x+1)(3-x)$ |
17.已知⊙O的半径为5cm,直线L上有一点P到圆心距离等于5,则直线L与⊙O的位置关系为( )
| A. | 相交 | B. | 相离 | C. | 相切 | D. | 相交或相切 |
4.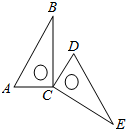 如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
 如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )| A. | 105° | B. | 120° | C. | 135° | D. | 150° |