题目内容
18.某学校游戏节活动中,设计了一个有奖转盘游戏,如图,A转盘被分成三个面积相等的扇形,B转盘被分成四个面积相等的扇形,每一个扇形都标有相应的数字,先转动A转盘,记下指针所指区域内的数字,再转动B转盘,记下指针所指区域内的数字(当指针在边界线上时,重新转动转盘,直到指针指向一个区域内为止)(1)请利用画树状图或列表的方法(只选其中一种),表示出转转盘可能出现的所有结果;
(2)如果将两次转转盘指针所指区域的数据相乘,乘积是无理数时获得一等奖,那么获得一等奖的概率是多少?
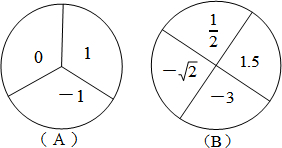
分析 (1)列表得出所有等可能的情况,进而可得转转盘可能出现的所有结果;
(2)找出乘积为无理数的情况数,即可求出一等奖的概率.
解答 解:(1)列表如下:
| 1.5 | -3 | -$\sqrt{2}$ | $\frac{1}{2}$ | |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1.5 | -3 | -$\sqrt{2}$ | $\frac{1}{2}$ |
| -1 | -1.5 | 3 | $\sqrt{2}$ | -$\frac{1}{2}$ |
(2)乘积是无理数的情况有2种,
则P(乘积为无理数)=$\frac{2}{12}$=$\frac{1}{6}$.
点评 此题考查的是用列表法或树状图法求概率.列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;树状图法适合两步或两步以上完成的事件;解题时要注意此题是放回实验还是不放回实验.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
8.观察下列4个命题:
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
(1)三角形的外角和是180°;
(2)三角形的三个内角中至少有两个锐角;
(3)如果x2y<0,那么y<0;
(4)(x-$\frac{1}{2}$)2=x2-$\frac{1}{4}$x+1.
其中真命题是( )
| A. | (1)(2) | B. | (2)(3) | C. | (2)(4) | D. | (3)(4) |
9.己知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的斜边上的高为( )
| A. | 12 | B. | 6 | C. | 5 | D. | $\frac{12}{5}$ |
6.某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如表:
未来20天内每天的价格y(元/件)与时间t(天)的函数关系式为y=$\frac{1}{4}$t+25(1≤t≤20且t为整数).
(1)认真分析表中的数据,用所学过的函数知识,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p(元).请求出p(元)与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
| 时间t(天) | 1 | 3 | 6 | 10 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | … |
(1)认真分析表中的数据,用所学过的函数知识,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p(元).请求出p(元)与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
13.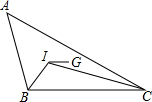 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
3.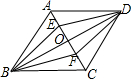 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )
如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )
 如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )
如图,O是菱形ABCD的对角线AC,BD的交点,E,F分别是OA,OC的中点,下列结论:①S△ADE=S△FOD,②四边形BFDE是中心对称图形;③△DEF是轴对称图形;④∠ADE=∠EDO,其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.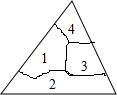 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
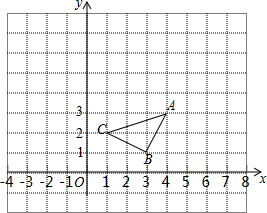 如图,将△ABC平移得到△A1B1C1,使A1点坐标为(-1,4)
如图,将△ABC平移得到△A1B1C1,使A1点坐标为(-1,4)