题目内容
6.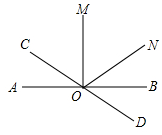 如图,直线AB与CD相交于点O,∠AOM=90°,且OM平分∠NOC.若∠BOC=4∠NOB,求∠MON的度数.
如图,直线AB与CD相交于点O,∠AOM=90°,且OM平分∠NOC.若∠BOC=4∠NOB,求∠MON的度数.
分析 设∠NOB=x,∠BOC=4x,根据垂直的定义、角平分线的定义得到∠MON=$\frac{1}{2}$∠CON=$\frac{3}{2}$x,∠BOM=∠MON+∠NOB=$\frac{3}{2}$x+x=90°,解方程求出x,进一步即可求得即∠MON的度数.
解答 解:设∠NOB=x,∠BOC=4x,
∵∠BOC=4∠NOB,
∴∠CON=∠COB-∠BON=4x-x=3x,
∵OM平分∠CON,
∴∠MON=$\frac{1}{2}$∠CON=$\frac{3}{2}$x,
∵∠AOM=90°,
∴∠BOM=∠MON+∠NOB=$\frac{3}{2}$x+x=90°,
∴x=36,
∴∠MON=$\frac{3}{2}$x=$\frac{3}{2}$×36°=54°,
即∠MON的度数为54°.
点评 本题考查的是对顶角、邻补角的概念和性质,掌握对顶角相等、垂直的定义、角平分线的定义是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
16.一艘轮船在静水中的最大航速为30km/h,江水的流速为v km/h,则轮船沿江逆流航行60km所用的时间是( )
| A. | $\frac{30-v}{60}$ | B. | $\frac{30+v}{60}$ | C. | $\frac{60}{30+v}$ | D. | $\frac{60}{30-v}$ |
17.化简(1+$\frac{1}{x-2}$)÷$\frac{x-1}{{x}^{2}-4x+4}$的结果是( )
| A. | x+2 | B. | x-1 | C. | $\frac{1}{x+2}$ | D. | x-2 |
14.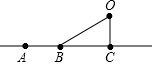 已知如图,则下列叙述不正确的是( )
已知如图,则下列叙述不正确的是( )
 已知如图,则下列叙述不正确的是( )
已知如图,则下列叙述不正确的是( )| A. | 点O不在直线AC上 | B. | 图中共有5条线段 | ||
| C. | 射线AB与射线BC是指同一条射线 | D. | 直线AB与直线CA是指同一条直线 |
1.下列命题中,属于真命题的是( )
| A. | 同位角相等 | B. | 任意三角形的外角一定大于内角 | ||
| C. | 多边形的内角和等于180° | D. | 同角或等角的余角相等 |
18.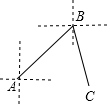 如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
 如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )
如图所示,一艘船在海上从A点出发,沿东北方向航行至点B,再从B点出发沿南偏东20°方向行至点C,则∠ABC的度数是( )| A. | 45° | B. | 65° | C. | 75° | D. | 90° |
 已知如图,直线AB、CD相交于点O,∠COE=90°.
已知如图,直线AB、CD相交于点O,∠COE=90°. 如图,锐角三角形ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知二次函数y═x2cosA-x+$\frac{1}{cosA}$的图象顶点与点(-2cosA,3cosA)关于y轴对称.延长AB到P,使AP=2AC,若以C为圆心,AC为半径的圆与以B为圆心、BP为半径的圆相外切.
如图,锐角三角形ABC中,∠A,∠B,∠C的对边分别是a,b,c,已知二次函数y═x2cosA-x+$\frac{1}{cosA}$的图象顶点与点(-2cosA,3cosA)关于y轴对称.延长AB到P,使AP=2AC,若以C为圆心,AC为半径的圆与以B为圆心、BP为半径的圆相外切.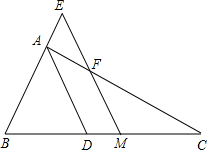 如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.
如图,△ABC中∠A的平分线为AD,M为BC的中点,过点M作ME∥AD交BA的延长线于E,交AC于F.