题目内容
 如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.
如图,直线AB与CD相交于O,OE⊥AB.OF⊥CD.(1)图中与∠COE互补的角是
(2)如果∠AOC=
| 1 |
| 4 |
考点:余角和补角
专题:
分析:(1)根据补角的定义,可得答案;
(2)根据∠AOC=
∠EOF,可得∠EOF=4∠AOC,根据余角的性质,可得∠AOF与∠COE的关系,根据角的和差,可得∠AOF与∠AOC的关系,根据余角的定义,可得∠AOC,根据对顶角相等,可得答案.
(2)根据∠AOC=
| 1 |
| 4 |
解答:解:(1)由OE⊥AB.OF⊥CD,得∠BOE=∠DOF=90°,
由等式的性质,得∠FOD+∠BOD=∠BOE+∠BOD即∠BOF=∠DOE,
由∠COE+∠EOD=180°,得∠COE与∠EOD互补,
由补角的性质,得∠COE与∠BOF互补,
故答案为:∠EOD、∠FOB;
(2)由∠AOC=
∠EOF,得∠EOF=4∠AOC.
由余角的性质,得∠COE=∠AOF,
由角的和差,得∠EOF=∠AOE+∠AOF+∠COE=4∠AOE.
由等式的性质,得
∠AOF+∠COE=3∠AOE.
2∠AOF=3∠AOE,
∠AOF=
∠AOE.
由余角的定义,得∠AOF+∠AOE=
∠AOE=∠FOC=90°.
解得∠AOE=36°.
由对顶角相等,得∠BOD=∠AOE=90°.
由等式的性质,得∠FOD+∠BOD=∠BOE+∠BOD即∠BOF=∠DOE,
由∠COE+∠EOD=180°,得∠COE与∠EOD互补,
由补角的性质,得∠COE与∠BOF互补,
故答案为:∠EOD、∠FOB;
(2)由∠AOC=
| 1 |
| 4 |
由余角的性质,得∠COE=∠AOF,
由角的和差,得∠EOF=∠AOE+∠AOF+∠COE=4∠AOE.
由等式的性质,得
∠AOF+∠COE=3∠AOE.
2∠AOF=3∠AOE,
∠AOF=
| 3 |
| 2 |
由余角的定义,得∠AOF+∠AOE=
| 5 |
| 2 |
解得∠AOE=36°.
由对顶角相等,得∠BOD=∠AOE=90°.
点评:本题考查了余角和补角,利用了余角和补角的定义,余角的性质和补角的性质.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知圆的半径是R,则圆内接正十边形的边长是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
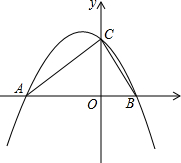 如图,抛物线y=-
如图,抛物线y=-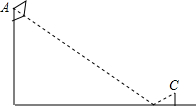 为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.
为测量学校操场上旗杆的高度,某数学活动小组设计如下测量方法:将镜子放在离旗杆(AB)27m的点E处,然后沿直线BE后退,使在点D处恰好看到旗杆顶端A在镜子中的像与镜子上的标记重合(如图),若DE=2.4m,观测者的眼睛离地面的高度CD为1.6m,求旗杆的高度.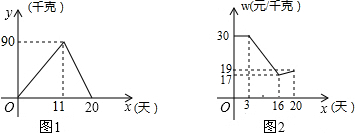
 已知二次函数的图象(0≤x≤3)如图所示,关于函数在所给变量取值范围内,函数y最小值=
已知二次函数的图象(0≤x≤3)如图所示,关于函数在所给变量取值范围内,函数y最小值=