题目内容
6.在△ADB和△AEC中,AD=AE,∠DAE=α,∠AEC=∠ADB=90°,BD=kCE,延长ED交BC于点F.(1)如图1,当k=1时,是否存在与BF相等的线段?若存在,请找出,并加以证明;若不存在,说明理由.
(2)如图2,当k≠1时,猜想并证明EC,ED,EF的数量关系(用含k,α的式子表示).
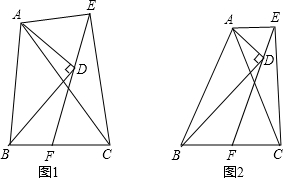
分析 (1)结论:BF=FC.首先证明△△BDN≌△CEM,得BN=CM,再证明△CFM≌△BFN,即可证明.
(2)结论:2EC•cos$\frac{1}{2}$α+ED=(k+1)EF.如图2中,作AH⊥EF于H,CM⊥EF于M,BN⊥EF于N.由△BDN∽△CEM,得$\frac{BD}{EC}$=$\frac{BN}{MC}$=k,由CM∥BN,得$\frac{FN}{FM}$=$\frac{BN}{CM}$=k,推出MF=$\frac{1}{k+1}$MN,再证明∠BDN=∠CEM=$\frac{1}{2}$α,推出EM=EC•cos$\frac{1}{2}$α,DN=BD•cos$\frac{1}{2}$α,EN=ED+DN=ED+BD•cos$\frac{1}{2}$α,MN=EN-EM=ED+k•EC•cos$\frac{1}{2}$α-EC•cos$\frac{1}{2}$α,FM=$\frac{1}{k+1}$•(ED+k•EC•cos$\frac{1}{2}$α-EC•cos$\frac{1}{2}$α),根据EF=EM+FM即可证明.
解答 解:(1)结论:BF=FC.理由如下,
如图1中,作CM⊥EF于M,BN⊥EF于N.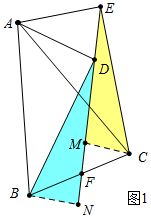
∵AE=AD,
∴∠AED=∠ADE,
∵∠ADB=∠AEC=90°,
∴∠ADE+∠BDN=90°,∠CEM+∠AED=90°,
∴∠CEM=∠BDN,
∵k=1,BD=kEC,
∴BD=EC,
∵BN⊥EF,CM⊥EF,
∴∠N=∠CME=90°,NB∥CM,
在△BDN和△CEM中,
$\left\{\begin{array}{l}{∠BDN=∠MEC}\\{∠BDN=∠MEC}\\{BD=EC}\end{array}\right.$,
∴△BDN≌△CEM,
∴BN=CM,
在△CFM和△BFN中,
$\left\{\begin{array}{l}{∠CMF=∠BNF}\\{∠CFM=∠BFN}\\{CM=BN}\end{array}\right.$,
∴△CFM≌△BFN,
∴BF=CF.
(2)结论:2EC•cos$\frac{1}{2}$α+ED=(k+1)EF.
如图2中,作AH⊥EF于H,CM⊥EF于M,BN⊥EF于N.
由(1)可知∠BDN=∠MEC,∵∠EMC=∠BND,
∴△BDN∽△CEM,
∴$\frac{BD}{EC}$=$\frac{BN}{MC}$=k,
∵CM∥BN,
∴$\frac{FN}{FM}$=$\frac{BN}{CM}$=k,
∴MF=$\frac{1}{k+1}$MN,
∵AE=AD,AH⊥ED,
∴∠HAE=∠HAD=$\frac{1}{2}$α,
∵∠EAH+∠AEH=90°,∠AEH+∠CEM=90°,
∴∠BDN=∠CEM=$\frac{1}{2}$α,
∴EM=EC•cos$\frac{1}{2}$α,DN=BD•cos$\frac{1}{2}$α,
∴EN=ED+DN=ED+BD•cos$\frac{1}{2}$α,
∴MN=EN-EM=ED+k•EC•cos$\frac{1}{2}$α-EC•cos$\frac{1}{2}$α,
∴FM=$\frac{1}{k+1}$•(ED+k•EC•cos$\frac{1}{2}$α-EC•cos$\frac{1}{2}$α),
∴EF=EM+FM=EC•cos$\frac{1}{2}$α+$\frac{1}{k+1}$(ED+k•EC•cos$\frac{1}{2}$α-EC•cos$\frac{1}{2}$α),
∴EF=$\frac{2}{k+1}$•EC•cos$\frac{1}{2}$α+$\frac{1}{k+1}$•ED,
∴2EC•cos$\frac{1}{2}$α+ED=(k+1)EF.
点评 本题考查全等三角形的判定和性质、相似三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识,学会添加常用辅助线,构造全等三角形或相似三角形,属于中考压轴题.

| A. | 点(2,4)在函数y=2x+4的图象上 | |
| B. | 已知甲,乙两组数据的个数相同且平均数相等,若甲组数据的方差S甲2=0.06,乙组数据的方差S乙2=0.105,则甲的波动比乙的波动小 | |
| C. | Rt△ABC的边a=3、b=4,则第三边c=5 | |
| D. | 二元一次方程组$\left\{\begin{array}{l}{x+y=3}\\{2x-3y=1}\end{array}\right.$的解是$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ |
| A. | -2 | B. | 2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |

 如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为110°.
如图,四边形ABCD内接于⊙O,E为CD延长线上一点.若∠B=110°,则∠ADE的度数为110°.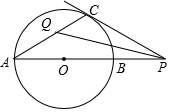 如图,P是⊙O的直线AB的延长线上的一点,PC与⊙O相切于点C,∠APC的角平分线交AC于点Q,则∠PQC=45°.
如图,P是⊙O的直线AB的延长线上的一点,PC与⊙O相切于点C,∠APC的角平分线交AC于点Q,则∠PQC=45°.