题目内容
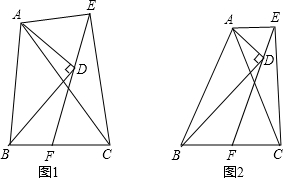
16.如图1,在△ABC中,∠ACB=90°,点P为△ABC内一点.
(1)连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长.
(2)如图3,连接PA,PB,PC,求PA+PB+PC的最小值.
小慧的作法是:以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,那么就将PA+PB+PC的值转化为CP+PM+MN的值,连接CN,当点P落在CN上时,此题可解.
请你参考小慧的思路,在图3中证明PA+PB+PC=CP+PM+MN.
并直接写出当AC=BC=4时,PA+PB+PC的最小值.
分析 (1)①连接PB,PC,将△BCP沿射线CA方向平移,得到△DAE,点B,C,P的对应点分别为点D,A,E,连接CE,据此画图即可;②连接BD、CD,构造矩形ACBD和Rt△CDE,根据矩形的对角线相等以及勾股定理进行计算,即可求得CE的长;
(2)以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.根据△PAM、△ABN都是等边三角形,可得PA+PB+PC=CP+PM+MN,最后根据当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,进而求得PA+PB+PC的最小值.
解答 解:(1)①补全图形如图所示;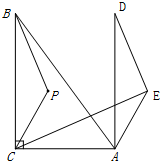
②如图,连接BD、CD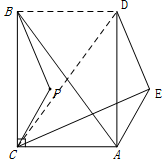
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中,CE=$\sqrt{C{D^2}-D{E^2}}$=$\sqrt{36-9}$=$\sqrt{27}$=$3\sqrt{3}$;
(2)证明:如图所示,以点A为旋转中心,将△ABP顺时针旋转60°得到△AMN,连接BN.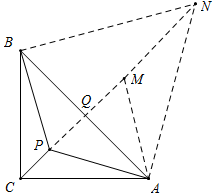
由旋转可得,△AMN≌△ABP,
∴MN=BP,PA=AM,∠PAM=60°=∠BAN,AB=AN,
∴△PAM、△ABN都是等边三角形,
∴PA=PM,
∴PA+PB+PC=CP+PM+MN,
当AC=BC=4时,AB=4$\sqrt{2}$,
当C、P、M、N四点共线时,由CA=CB,NA=NB可得CN垂直平分AB,
∴AQ=$\frac{1}{2}$AB=2$\sqrt{2}$=CQ,NQ=$\sqrt{3}$AQ=2$\sqrt{6}$,
∴此时CN=CP+PM+MN=PA+PB+PC=$2\sqrt{2}+2\sqrt{6}$.
点评 本题属于几何变换综合题,主要考查了旋转和平移的性质、全等三角形的判定与性质、矩形的性质以及勾股定理的综合应用,解决问题的关键是作辅助线构造等边三角形和全等三角形,依据图形的性质进行计算求解.

| A. | 先向左平移1个单位,再向上平移2个单位 | |
| B. | 先向左平移1个单位,再向下平移2个单位 | |
| C. | 先向右平移1个单位,再向上平移2个单位 | |
| D. | 先向右平移1个单位,再向下平移2个单位 |
 实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b.
实数a、b在数轴上的位置如图所示,则化简|a+2b|-|a-b|的结果为2a+b. 一个圆形零件的部分碎片如图所示.请你利用尺规作图找到圆心O.(要求:不写作法,保留作图痕迹)
一个圆形零件的部分碎片如图所示.请你利用尺规作图找到圆心O.(要求:不写作法,保留作图痕迹)