题目内容
已知等腰△ABC中,AB=AC=13,△ABC的面积为60,求△ABC内切圆的半径.
考点:三角形的内切圆与内心
专题:
分析:设△ABC内切圆的半径为R,根据等腰三角形的性质得出BD=DC,根据三角形面积和勾股定理得出方程组,求出BC的值,再根据三角形的面积得出关于R的方程,求出即可.
解答: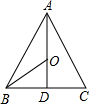 解:设△ABC内切圆的半径为R,
解:设△ABC内切圆的半径为R,
如图,AD⊥BC于D,
∵AB=AC,
∴BD=DC,O在AD上,
设BD=DC=x,AD=y,
∵AB=AC=13,△ABC的面积为60,
∴
解得:
或
,
即BC=24,AD=5或BC=10,AD=12,
由三角形面积公式得:
AC×R+
BC×R+
AC×R=60,
∴R=
或
,
∴△ABC内切圆的半径是R=
或
.
 解:设△ABC内切圆的半径为R,
解:设△ABC内切圆的半径为R,如图,AD⊥BC于D,
∵AB=AC,
∴BD=DC,O在AD上,
设BD=DC=x,AD=y,
∵AB=AC=13,△ABC的面积为60,
∴
|
解得:
|
|
即BC=24,AD=5或BC=10,AD=12,
由三角形面积公式得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴R=
| 12 |
| 5 |
| 10 |
| 3 |
∴△ABC内切圆的半径是R=
| 12 |
| 5 |
| 10 |
| 3 |
点评:本题考查了三角形的内心和内切圆,等腰三角形的性质,三角形的面积的应用,能求出BC的值和得出关于R的方程是解此题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
若-1是方程x2+mx+n=0的一个根,则m-n的值为( )
| A、-2 | B、2 | C、-1 | D、1 |
 如图,已知DF⊥AB于点F,且∠A=45°,∠D=30°,求∠ACB的度数.
如图,已知DF⊥AB于点F,且∠A=45°,∠D=30°,求∠ACB的度数. 图中,等边△ABC的边长为acm,D、E分别是AB、AC上的点,将△ADE沿DE折叠,点A落在点A′处,且点A′在△ABC的外部,那么阴影部分图形的周长为( )cm.
图中,等边△ABC的边长为acm,D、E分别是AB、AC上的点,将△ADE沿DE折叠,点A落在点A′处,且点A′在△ABC的外部,那么阴影部分图形的周长为( )cm. 如图,P为⊙O的直径AB上一点,M、N在半圆
如图,P为⊙O的直径AB上一点,M、N在半圆