题目内容
 如图,P为⊙O的直径AB上一点,M、N在半圆
如图,P为⊙O的直径AB上一点,M、N在半圆 |
| AB |
考点:垂径定理,含30度角的直角三角形,勾股定理
专题:计算题
分析:延长NP交⊙O于Q,作OH⊥NQ于H,连结MQ,ON,如图,由∠APM=∠NPB,∠APQ=∠NPB得到∠APM=∠APQ,利用圆的对称性得到点M与点Q关于AB对称,则PM=PQ,所以PN+PM=PQ+PN=NQ,在Rt△OPH中利用含30度的直角三角形三边的关系得到OH=1,则在Rt△OHN中可勾股定理计算出NH=2
,然后根据垂径定理得到NH=QH,NQ=2NH=4
,即可得到PN+PM的值.
| 6 |
| 6 |
解答:解:延长NP交⊙O于Q,作OH⊥NQ于H,连结MQ,ON,如图,
∵∠APM=∠NPB,
而∠APQ=∠NPB,
∴∠APM=∠APQ,
∴点M与点Q关于AB对称,
∴PM=PQ,
∴PN+PM=PQ+PN=NQ,
在Rt△OPH中,∵OP=2,∠OPH=30°,
∴OH=1,
在Rt△OHN中,∵OH=1,ON=5,
∴NH=
=2
,
∵OH⊥NQ,
∴NH=QN,
∴NQ=2NH=4
,
∴PN+PM的值为4
.

∵∠APM=∠NPB,
而∠APQ=∠NPB,
∴∠APM=∠APQ,
∴点M与点Q关于AB对称,
∴PM=PQ,
∴PN+PM=PQ+PN=NQ,
在Rt△OPH中,∵OP=2,∠OPH=30°,
∴OH=1,
在Rt△OHN中,∵OH=1,ON=5,
∴NH=
| ON2-OH2 |
| 6 |
∵OH⊥NQ,
∴NH=QN,
∴NQ=2NH=4
| 6 |
∴PN+PM的值为4
| 6 |
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了含30度的直角三角形三边的关系和勾股定理.

练习册系列答案
相关题目
 美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )
美化城市、改善人们的居住环境已成为城市建设的一项重要内容.某区近几年来,通过拆迁旧房、植草、栽树、修建公园等措施,使城区绿地面积不断增加,根据图中所提供的信息,下列说法错误的是( )| A、2009年该区的绿地面积为420公顷 |
| B、2011年的绿地面积增长最快 |
| C、从2009年到2012年,每年绿地面积的增长率都在增长 |
| D、从2009年到2012年,每年的绿地面积都在增长 |
 如图,BD=DC,AB=AC,∠BAC=70°,则∠BAD=( )
如图,BD=DC,AB=AC,∠BAC=70°,则∠BAD=( )| A、40° | B、70° |
| C、30° | D、35° |
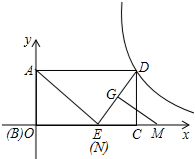 如图,在平面直角坐标系中,已知矩形ABCD,E是BC上一点,∠AED=90°,AB=6,SIN∠AEB=
如图,在平面直角坐标系中,已知矩形ABCD,E是BC上一点,∠AED=90°,AB=6,SIN∠AEB= 如图所示,将直角边长为6
如图所示,将直角边长为6 已知二次函数y=x2+bx-1的图象经过点(3,2).
已知二次函数y=x2+bx-1的图象经过点(3,2). 如图,该图中不同的线段数共有
如图,该图中不同的线段数共有