题目内容
17.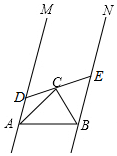 已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.若AB=10,AD=4,则BE=6.
已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.若AB=10,AD=4,则BE=6.
分析 在线段AB上截取AF=AD,连接FC,只要证明△ADC≌△AFC(SAS),△CBF≌△CBE(AAS)即可解决问题.
解答  解:如图中,在线段AB上截取AF=AD,连接FC.
解:如图中,在线段AB上截取AF=AD,连接FC.
∵AC,BC分别平分∠MAB,∠NBA,
∴∠1=∠2,∠3=∠4,
在△ADC和△AFC中,
∵$\left\{\begin{array}{l}{AD=AF}\\{∠1=∠2}\\{AC=AC}\end{array}\right.$,
∴△ADC≌△AFC(SAS),
∴∠ADC=∠AFC,
∵MA∥NB,
∴∠ADC+∠6=180°,
又∵∠5+∠AFC=180°,
∴∠5=∠6.
在△CBF和△CBE中,
$\left\{\begin{array}{l}{∠5=∠6}\\{∠3=∠4}\\{BC=BC(公共边)}\end{array}\right.$,
∴△CBF≌△CBE(AAS),
∴BF=BE,
∵AF+BF=AB,
∴AD+BE=AB,
∵AB=10,AD=4,
∴BE=6,
故答案为:6.
点评 本题考查了全等三角形的性质和判定、角平分线的定义等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
13.已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0)、(x2,0),且1<x2<2,与y轴正半轴的交点在(0,2)下方,在下列结论中:①b<0,②4a-2b+c=0,③2a-b+1<0,④b<a<c.其中正确结论是( )
| A. | ①② | B. | ③④ | C. | ①②③ | D. | ①②④ |
8.下列说法:
①若|-a|+a=0,则a≤0;
②两个有理数的和必定大于其中一个加数;
③互为相反数的两个数相乘所得的积是负数;
④立方根等于本身的数是0、1.
其中说法正确的有( )个.
①若|-a|+a=0,则a≤0;
②两个有理数的和必定大于其中一个加数;
③互为相反数的两个数相乘所得的积是负数;
④立方根等于本身的数是0、1.
其中说法正确的有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9x5,11x6,….按照上述规律,第2 015个单项式是( )
| A. | 2 015x2015 | B. | 4 029x2014 | C. | 4 029x2015 | D. | 4 031x2015 |
12.若3xa-2-4=0是关于x的一元一次方程,则a=( )
| A. | 0 | B. | 3 | C. | 4 | D. | 1 |
2.下列各式中,无意义的是( )
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{(-2)^{2}}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{-\frac{1}{4}}$ |
9.三角形的一个内角等于其余两个内角的和,则这个三角形是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 锐角三角形 |
6.下列说法正确的是( )
| A. | 正负号相反的两个数互为相反数 | |
| B. | 数轴上原点两侧的两个点所表示的数是互为相反数 | |
| C. | 相反数和我们以前学过的倒数是一样的 | |
| D. | 只有正负号不同的两个数称互为相反数,零的相反数是零 |