题目内容
5.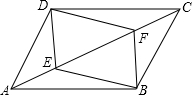 如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
如图,已知四边形ABCD是平行四边形,BE∥DF,且分别交对角线AC于点E,F,连接DE,BF.求证:四边形DEBF是平行四边形.
分析 由平行四边形的性质和已知条件证明△CEB≌△AFD,所以可得BE=DF,进而证明四边形BFED是平行四边形.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=CB,AD∥CB,
∴∠BCE=∠DAF
又∵BE∥DF,
∴∠BEC=∠DFA
在△CEB和△AFD中,$\left\{\begin{array}{l}{∠CEB=∠DAF}\\{∠BEC=∠DFA}\\{BC=DA}\end{array}\right.$,
∴△CEB≌△AFD(AAS)
∴BE=DF
∴四边形DEBF为平行四边形.
点评 本题考查了平行四边形的判定和性质,全等三角形的判定和性质,熟练掌握这些定理是解题的关键.

练习册系列答案
相关题目
13.直线y=2x-1沿y轴向下平移3个单位,则平移后直线与x轴的交点坐标为( )
| A. | (-2,0) | B. | (2,0) | C. | (4,0) | D. | (-1,0) |
10.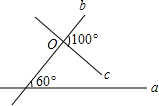 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
 平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )
平面上直线a、c与b相交(数据如图),当直线c绕点O旋转某一角度时与a平行,则旋转的最小度数是( )| A. | 60° | B. | 50° | C. | 40° | D. | 30° |
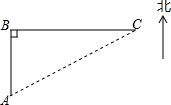 如图,在海上观察所A处,我边防海警发现正北60海里的B处,有一可疑船只正在往正东方向80海里的C处行驶,速度为40海里/小时,我边防海警立即派海警船从A处出发,沿AC方向行驶前往C处拦截,当可疑船只行驶到C处时,海警船也同时到达并将其截住,求海警船的速度.
如图,在海上观察所A处,我边防海警发现正北60海里的B处,有一可疑船只正在往正东方向80海里的C处行驶,速度为40海里/小时,我边防海警立即派海警船从A处出发,沿AC方向行驶前往C处拦截,当可疑船只行驶到C处时,海警船也同时到达并将其截住,求海警船的速度.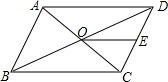 如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为36cm,则△DOE周长是( )cm.
如图,平行四边形ABCD的对角线AC,BD相交于点O,点E是CD的中点,△ABD的周长为36cm,则△DOE周长是( )cm.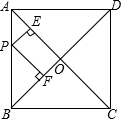 如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.
如图,正方形ABCD中,对角线BD长为15cm.P是线段AB上任意一点,则点P到AC,BD的距离之和等于$\frac{15}{2}$cm.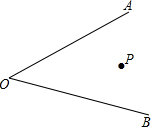 在学完全等三角形后,李老师给出了下列题目:
在学完全等三角形后,李老师给出了下列题目: 如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.
如图,边长为1的菱形形ABCD中,∠DAB=60°,连接对角线AC,以AC为边作第二个菱形ACEF,使∠FAC=60°,连接AE,再以AE为边作第三个菱形AEGH,使∠HAE=60°…,按此规律推测,所作的第2015个菱形的边长是$(\sqrt{3})^{2014}$.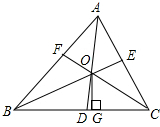 如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.
如图,△ABC各角的平分线AD、BE、CF交于O,作OG⊥BC于G,求证:∠BOD=∠COG.