题目内容
4.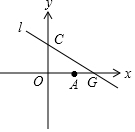 如图,点O为坐标原点,直线l:y=kx+2(k<0)与x轴、y轴分别交于点G(m,0),点C(0,2),B是直线l上的一点,且点A(2,0).
如图,点O为坐标原点,直线l:y=kx+2(k<0)与x轴、y轴分别交于点G(m,0),点C(0,2),B是直线l上的一点,且点A(2,0).(1)若∠GCA=15°,m>2,求直线l的解析式;
(2)若AB⊥BC,AB=1,求m的值;
(3)若点B在第一象限,且AB=AO,△OBC是等腰三角形,直接写出点B的坐标.
分析 (1)求出点G坐标,利用待定系数法即可解决问题;
(2)分两种情形①m>2时,如图2中,Rt△GOC∽△Rt△GBA,②0<m<2时,如图3中,分别求解即可.
(3)分三种情形讨论求解即可.①当OC=OB时,△OBA是等边三角形时,△OBC是等腰三角形,此时B(1,$\sqrt{3}$).②当BC=OB时,易知B的纵坐标为1,设横坐标为x,则有12+(2-x)2=22.③当CO=CB时,BC∥x轴,不符合题意.
解答 解:(1)如图1中,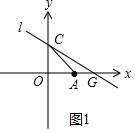
∵OC=OA=2,
∴∠OCA=∠OAC=45°,
∵∠GCA=15°,m>2,
∴∠GCO=60°,
在Rt△GOC中,CO=2,
∴OG=2$\sqrt{3}$,
∴G(2$\sqrt{3}$,0),
设直线GC的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{b=2}\\{2\sqrt{3}k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=2}\end{array}\right.$,
∴y=-$\frac{\sqrt{3}}{3}$x+2.
(2)①m>2时,如图2中,Rt△GOC∽△Rt△GBA,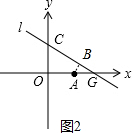
∵AB=1,OC=2,AG=m-2,
∴4+m2=(4-2m)2,
解得m=$\frac{8+2\sqrt{7}}{3}$或$\frac{8-2\sqrt{7}}{3}$(舍弃),
②0<m<2时,如图3中,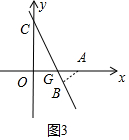
同理可得m=$\frac{8-2\sqrt{7}}{3}$,
∴m=$\frac{8+2\sqrt{7}}{3}$或$\frac{8-2\sqrt{7}}{3}$.
(3)①当OC=OB时,△OBA是等边三角形时,△OBC是等腰三角形,此时B(1,$\sqrt{3}$),
②当BC=OB时,易知B的纵坐标为1,设横坐标为x,
则有12+(2-x)2=22,
解得x=2$±\sqrt{3}$,
∴B(2+$\sqrt{3}$,1)或(2-$\sqrt{3},1$),
③当CO=CB时,BC∥x轴,不符合题意.
综上所述,满足条件的点B坐标为(1,$\sqrt{3}$)或(2-$\sqrt{3}$,1)或(2+$\sqrt{3}$,1).
点评 本题考查一次函数综合题、待定系数法、相似三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会构建方程,学会用分类讨论的思想思考问题,属于中考压轴题.

| A. | x+1>2 | B. | x2>9 | C. | 2x+y≤5 | D. | $\frac{1}{x}$>3 |
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
| A. | 30个 | B. | 80个 | C. | 90个 | D. | 120个 |
 如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )
如图,点A,B,C,D在数轴上,其中表示互为相反数的点是( )| A. | 点A与点D | B. | 点B与点D | C. | 点A与点C | D. | 点B与点C |
 如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )
如图,在平面直角坐标系中,点A在抛物线y=x2-2x+3上运动.过点A作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为( )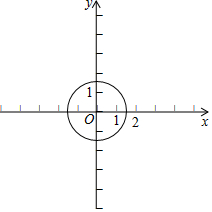 在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.
在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(-2,-2),($\sqrt{2}$,$\sqrt{2}$),…,都是梦之点,显然梦之点有无数个.