题目内容
14.先化简:(x-1-$\frac{3}{x+1}$)$÷\frac{{x}^{2}-4x+4}{x+1}$,然后从满足-2<x≤2的整数值中选择一个你喜欢的数代入求值.分析 先将原式化简,然后根据分式有意义的条件即可选出x的值代入.
解答 解:原式=$\frac{(x-1)(x+1)-3}{x+1}$×$\frac{x+1}{(x-2)^{2}}$
=$\frac{(x+2)(x-2)}{x+1}$•$\frac{x+1}{(x-2)^{2}}$
=$\frac{x+2}{x-2}$
∵-2<x≤2且x为整数,
∴若分式有意义,x只能取0,1,
当x=0时,
∴原式=-1(或当x=1时,原式=-3)
点评 本题考查分式的化简求值,解题的关键是熟练运用分式的运算法则,本题属于基础题型.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
5. 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )
如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y=$\frac{k}{x}$在第一象限的图象经过小正方形右下顶点E.若OB2-BE2=10,则k的值是( )| A. | 3 | B. | 4 | C. | 5 | D. | 4$\sqrt{5}$ |
2.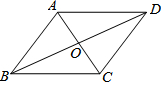 如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
 如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )
如图,平行四边形ABCD的对角线AC与BD相交于点O,要使它成为矩形,需再添加的条件是( )| A. | AO=OC | B. | AC=BD | C. | AC⊥BD | D. | BD平分∠ABC |
9.运用乘法公式计算(x-2)2的结果是( )
| A. | x2-4x+4 | B. | x2-4 | C. | x2+4x+4 | D. | x2-2x+4 |
4.已知一组数据:1,2,6,3,3,下列说法错误的是( )
| A. | 众数是3 | B. | 中位数是6 | C. | 平均数是3 | D. | 方差是2.8 |
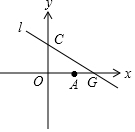 如图,点O为坐标原点,直线l:y=kx+2(k<0)与x轴、y轴分别交于点G(m,0),点C(0,2),B是直线l上的一点,且点A(2,0).
如图,点O为坐标原点,直线l:y=kx+2(k<0)与x轴、y轴分别交于点G(m,0),点C(0,2),B是直线l上的一点,且点A(2,0).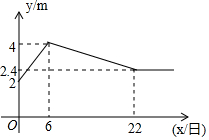 如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.
如图,是皖韵水库进入5月份以来的水位y米与x日的函数图象,为了避免过度捕捞,当水位低于3米时就不适宜渔船打捞作业,根据图象可知,5月份能打捞的天数有( )天.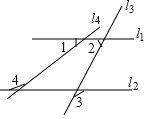 已知直线l1∥l2,∠1和∠2互余,∠3=121°,则∠4=149°.
已知直线l1∥l2,∠1和∠2互余,∠3=121°,则∠4=149°.