题目内容
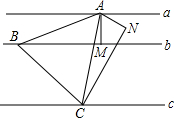 有一组平行线a∥b∥c,过点A作AM⊥b于M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线c于点C,在直线b上取点B使BM=CN,则△ABC为
有一组平行线a∥b∥c,过点A作AM⊥b于M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN交直线c于点C,在直线b上取点B使BM=CN,则△ABC为考点:全等三角形的判定与性质,平行线之间的距离,等边三角形的判定与性质
专题:
分析:证明△ABM≌△ACN(SAS),即可证出AB=AC,∠BAC=∠CAN=60°,证出世纪星ABC为等边三角形;在图1中,过点N作HG⊥a于H,交c于点G,由勾股定理先求出CN的值就可以求出AC的值.
解答:解:∵AM⊥b,CN⊥AN,
∴∠AMB=∠ANC=90°,
在△ABM与△ACN中,
,
∴△ABM≌△ACN(SAS),
∴∠BAM=∠CAN,AB=AC;
∴∠BAC=∠MAN=60°,
∴△ABC为等边三角形.
故答案为:等边.
如图1,过点N作HG⊥a于H,交c于点G,
 ∴∠AHN=∠NGC=90°.
∴∠AHN=∠NGC=90°.
∵∠MAN=60°,
∴∠HAN=30°,
∴HN=AN,∠ANH=60°,
∵AM=AN=1,
∴HN=0.5.
∴HG=2.5.
∵CN⊥AN,
∴∠ANC=90°,
∴∠ANH+∠CNG=90°,
∴∠CNG=30°,
∴CN=2CG,
在Rt△CGN中,由勾股定理,得
4CG2-CG2=
,CG=
∴CN=
在Rt△ANC中,由勾股定理,得
AC2=(
)2+1,
∴AC=
;
故答案为:
.
∴∠AMB=∠ANC=90°,
在△ABM与△ACN中,
|
∴△ABM≌△ACN(SAS),
∴∠BAM=∠CAN,AB=AC;
∴∠BAC=∠MAN=60°,
∴△ABC为等边三角形.
故答案为:等边.
如图1,过点N作HG⊥a于H,交c于点G,
 ∴∠AHN=∠NGC=90°.
∴∠AHN=∠NGC=90°.∵∠MAN=60°,
∴∠HAN=30°,
∴HN=AN,∠ANH=60°,
∵AM=AN=1,
∴HN=0.5.
∴HG=2.5.
∵CN⊥AN,
∴∠ANC=90°,
∴∠ANH+∠CNG=90°,
∴∠CNG=30°,
∴CN=2CG,
在Rt△CGN中,由勾股定理,得
4CG2-CG2=
| 25 |
| 4 |
5
| ||
| 6 |
∴CN=
5
| ||
| 3 |
在Rt△ANC中,由勾股定理,得
AC2=(
5
| ||
| 3 |
∴AC=
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |
点评:本题考查了全等三角形的判定与性质和等边三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
四个角都相等,且邻边相等的四边形是( )
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
 已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.
已知∠AOB=40°,∠AOB的余角为∠AOC,∠AOB的补角为∠BOD,OM平分∠AOC,ON平分∠BOD.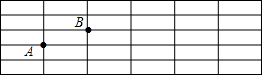 如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( )
如图,在长方形网格中,每个小长方形的长为3,宽为1,A、B两点在网格格点上.若点C也在网格格点上,以A、B、C为顶点的三角形面积为3,则满足条件的点C有( ) 在△ABC中,BD为AC边的垂线,CD=2,AD=4,tan∠ABC=
在△ABC中,BD为AC边的垂线,CD=2,AD=4,tan∠ABC=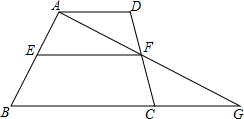 如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且
如图,已知在梯形ABCD中,AD∥BC,E、F分别在AB、CD边上的点,AF交BC的延长线于点G,且