题目内容
在△ABC中，BD为AC边的垂线，CD=2，AD=4，tan∠ABC=| 6 |
| 7 |
考点：解直角三角形
专题：计算题
分析：作CH⊥AB于H，如图在Rt△BCH中，利用正切的定义得到tan∠HBC=
=
，则可设CH=6x，BH=7x，再根据勾股定理得到BC=
x，然后证明Rt△ABD∽Rt△ACH，利用相似比得
=
，再根据比例的性质可计算出AB．
| CH |
| BH |
| 6 |
| 7 |
| 85 |
| AB |
| 4+2 |
| 6x | ||
|
解答：解：作CH⊥AB于H，如图，
在Rt△BCH中，tan∠HBC=
=
，
设CH=6x，则BH=7x，
∴BC=
=
x，
∵BD⊥AD，∠HAC=∠DAB，
∴Rt△ABD∽Rt△ACH，
∴
=
，即
=
，
∴AB=
．
在Rt△BCH中，tan∠HBC=
| CH |
| BH |
| 6 |
| 7 |
设CH=6x，则BH=7x，
∴BC=
| BH2+CH2 |
| 85 |
∵BD⊥AD，∠HAC=∠DAB，
∴Rt△ABD∽Rt△ACH，
∴
| AB |
| AC |
| CH |
| BC |
| AB |
| 4+2 |
| 6x | ||
|
∴AB=
36
| ||
| 85 |
点评：本题考查了解直角三角形：在直角三角形中，由已知元素求未知元素的过程就是解直角三角形．也考查了相似三角形的判定与性质．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
某中学为了提高学生的跳远能力，通过一个月的锻炼，学校对九（1）班的45名学生进行测试，成绩如下表：
这个班学生跳远成绩的中位数和众数分别是（ ）
| 跳远成绩（cm） | 160 | 170 | 180 | 190 | 200 | 220 |
| 人数 | 3 | 9 | 6 | 9 | 15 | 3 |
| A、190，200 |
| B、9，9 |
| C、9，15 |
| D、185，200 |
用字母表示如图长方形中空白部分的面积．（要求列示并化简）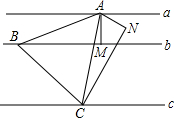
有一组平行线a∥b∥c，过点A作AM⊥b于M，作∠MAN=60°，且AN=AM，过点N作CN⊥AN交直线c于点C，在直线b上取点B使BM=CN，则△ABC为
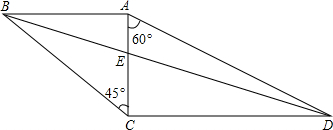如图，将三角尺ABC、ACD摆放在一起，设BD交AC于点E，则△ABE∽
如图，数轴的单位长度为1，如果B、C表示的数的和为2，那么A、D表示的数的和是（ ）| A、5 | B、4 | C、3 | D、2 |
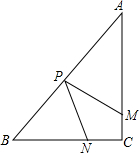如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3com，动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A、B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM、PN，设移动时间为t秒（0＜t＜2.5）．