题目内容
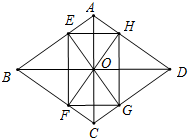 如图,四边形ABCD为菱形,通过它的对角线的交点O作AB、BC的垂线,与AB、BC、CD、DA分别交于点E、F、G、H,求证:四边形EFGH为矩形.
如图,四边形ABCD为菱形,通过它的对角线的交点O作AB、BC的垂线,与AB、BC、CD、DA分别交于点E、F、G、H,求证:四边形EFGH为矩形.考点:菱形的性质,矩形的判定
专题:证明题
分析:根据菱形的中心对称性可得OE=OG,OF=OH,然后根据对角线互相平分的四边形的平行四边形可得四边形EFGH为平行四边形,再根据菱形的高相等可得EG=FH,然后根据对角线相等的平行四边形的矩形证明.
解答:证明:∵四边形ABCD为菱形,O为对角线的交点,
∴OE=OG,OF=OH,
∴四边形EFGH为平行四边形,
∵EG、FH分别与AB、BC垂直,
∴EG、FH都是菱形的高,
∴EG=FH,
∴四边形EFGH为矩形.
∴OE=OG,OF=OH,
∴四边形EFGH为平行四边形,
∵EG、FH分别与AB、BC垂直,
∴EG、FH都是菱形的高,
∴EG=FH,
∴四边形EFGH为矩形.
点评:本题考查了菱形的性质,矩形的判定,考虑利用菱形的中心对称性求解更简便.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
绝值大于1而小于5的整数有( )
| A、7个 | B、6个 | C、5个 | D、4个 |
 如图,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=5,BC=12,求AD的长.
如图,△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若AC=5,BC=12,求AD的长.