题目内容
如图，△ABC中，∠ACB=90°，CD⊥AB，垂足为D，若AC=5，BC=12，求AD的长．考点：勾股定理
专题：
分析：根据勾股定理求出AB的长，再根据△CDA∽△BCA，列出
=
，求出AD的长．
| AD |
| AC |
| AC |
| AB |
解答：解：在Rt△ABC中，AB=
=13，
∵∠A=∠A，∠CDA=∠BCA，
∴△CDA∽△BCA，
∴
=
，
∴
=
，
∴AD=
．
| 52+122 |
∵∠A=∠A，∠CDA=∠BCA，
∴△CDA∽△BCA，
∴
| AD |
| AC |
| AC |
| AB |
∴
| AD |
| 5 |
| 5 |
| 13 |
∴AD=
| 25 |
| 13 |
点评：本题考查了勾股定理和三角形相似，找到对应边，求出相似比是解题的关键．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
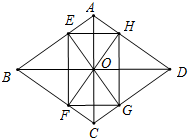如图，四边形ABCD为菱形，通过它的对角线的交点O作AB、BC的垂线，与AB、BC、CD、DA分别交于点E、F、G、H，求证：四边形EFGH为矩形．下列函数中，y随x的增大而减小的是（ ）
| A、y=-3x | ||
| B、y=3x-4 | ||
C、y=-
| ||
D、y=
|
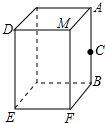如图，长方体盒子的长、宽、高分别是6cm，8cm，30cm．在AB中点C处有一小孔，若盒壁的厚度和小孔的大小忽略不计，则从C处能放入长方体内木棒的最大长度是