题目内容
已知：a=10000，b=9999，则a2+b2-2ab-6a+6b+9为 ．
考点：因式分解的应用
专题：计算题
分析：利用完全平方公式把原式变形得到a2+b2-2ab-6a+6b+9=（a-b）2-6（a-b）+9=[（a-b）-3]2，然后把a与b的值代入计算即可．
解答：解：∵a=10000，b=9999，
∴a2+b2-2ab-6a+6b+9=（a-b）2-6（a-b）+9
=[（a-b）-3]2
=（10000-9999-3）2
=4．
故答案为4．
∴a2+b2-2ab-6a+6b+9=（a-b）2-6（a-b）+9
=[（a-b）-3]2
=（10000-9999-3）2
=4．
故答案为4．
点评：本题考查了因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．
练习册系列答案
相关题目
下列各式运算正确的是（ ）
| A、a2+a3=a5 |
| B、a2•a3=a5 |
| C、（ab2）3=ab6 |
| D、a10÷a2=a5 |
如图，已知∠DAB=∠CBE=90°，点E是线段AB的中点，CE平分∠DCB且与DA的延长线相交于点F，求证：DE平分∠FDC．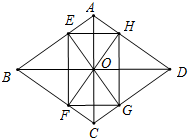
如图，四边形ABCD为菱形，通过它的对角线的交点O作AB、BC的垂线，与AB、BC、CD、DA分别交于点E、F、G、H，求证：四边形EFGH为矩形．