题目内容
已知△ABC的三条边长分别为6,8,12,过△ABC任一顶点画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( )
| A、6条 | B、7条 | C、8条 | D、9条 |
考点:等腰三角形的判定
专题:
分析:不妨设AB=6,AC=8,BC=12,分别作三边的垂直平分线,则可得三条,再分以AB、AC为腰和底进行讨论,可得出结论.
解答:解:不妨设AB=6,AC=8,BC=12,分别作三边的垂直平分线,
如图1,则BD=AD,EA=EC,FB=FC,可知AE、BF、AD满足条件,
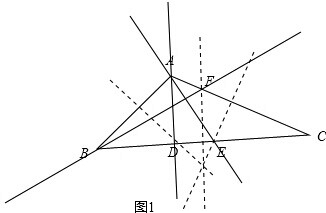
当AB为腰时,以点A为圆心,AB为半径画圆,分别交BC、AC于点G、H,
以B为圆心,AB为半径,交BC于点J,如图2,则AB=AG,AB=AH,BA=BJ,满足条件
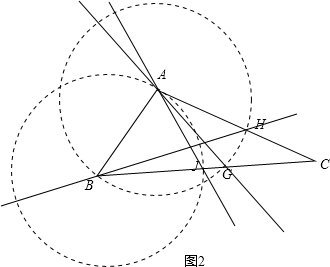
当AC为腰时,如图3,以点C为圆心,CA为半径画圆,交BC于点M,则CA=CM,满足条件,
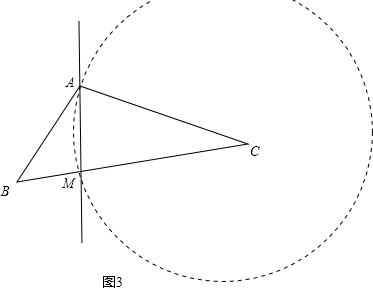
当A为圆心AC为半径画圆时,与AB、BC都没有交点,
因为BC为最长的边,所以不可能存在以BC为腰的等腰三角形,
综上可知满足条件的直线共有7条,
故选B.
如图1,则BD=AD,EA=EC,FB=FC,可知AE、BF、AD满足条件,

当AB为腰时,以点A为圆心,AB为半径画圆,分别交BC、AC于点G、H,
以B为圆心,AB为半径,交BC于点J,如图2,则AB=AG,AB=AH,BA=BJ,满足条件

当AC为腰时,如图3,以点C为圆心,CA为半径画圆,交BC于点M,则CA=CM,满足条件,

当A为圆心AC为半径画圆时,与AB、BC都没有交点,
因为BC为最长的边,所以不可能存在以BC为腰的等腰三角形,
综上可知满足条件的直线共有7条,
故选B.
点评:本题主要考查等腰三角形的判定,利用垂直平分线的性质及圆的性质找到满足条件的直线是解题的关键.

练习册系列答案
相关题目
下列各式运算正确的是( )
| A、a2+a3=a5 |
| B、a2•a3=a5 |
| C、(ab2)3=ab6 |
| D、a10÷a2=a5 |
 如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC.
如图,已知∠DAB=∠CBE=90°,点E是线段AB的中点,CE平分∠DCB且与DA的延长线相交于点F,求证:DE平分∠FDC. 如图是由几个小立方块所搭几何体从上面看到的图形,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体从正面、从左面看到的图形.
如图是由几个小立方块所搭几何体从上面看到的图形,小正方形中的数字表示在该位置小立方块的个数,请画出相应几何体从正面、从左面看到的图形.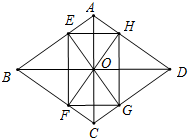 如图,四边形ABCD为菱形,通过它的对角线的交点O作AB、BC的垂线,与AB、BC、CD、DA分别交于点E、F、G、H,求证:四边形EFGH为矩形.
如图,四边形ABCD为菱形,通过它的对角线的交点O作AB、BC的垂线,与AB、BC、CD、DA分别交于点E、F、G、H,求证:四边形EFGH为矩形.