题目内容
5.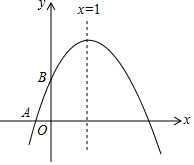 如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)之间(不包括端点).有下列结论:①当x>3时,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正确的结论有( )
如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2)和(0,3)之间(不包括端点).有下列结论:①当x>3时,y<0;②n=c-a;③3a+b>0;④-1<a<-$\frac{2}{3}$.其中正确的结论有( )| A. | 1 个 | B. | 2 个 | C. | 3 个 | D. | 4 个 |
分析 由抛物线与x轴的交于点A(-1,0)且对称轴为x=1,知函数图象与x轴的另一个交点为(3,0),结合图象可判断①;由对称轴为x=-$\frac{b}{2a}$=1得b=-2a,将其代入n=a+b+c可判断②;由开口方向知a<0,将b=-2a代入3a+b即可判断③;由图象过(-1,0)知a-b+c=0,将b=-2a代入可得c=-3a,结合抛物线与y轴的交点在(0,2)和(0,3)之间(不包括端点)得2<c<3,即2<-3a<3,从而判断④.
解答 解:∵函数图象与x轴交于点A(-1,0),且对称轴为x=1,
则函数图象与x轴的另一个交点为(3,0),
∴当x>3时,y<0,故①正确;
∵抛物线的对称轴为x=-$\frac{b}{2a}$=1,
∴b=-2a,
∵顶点坐标为(1,n),
∴n=a+b+c=a-2a+c,即n=c-a,故②正确;
∵抛物线的开口向下,
∴a<0,
∵b=-2a,
∴3a+b=3a-2a=a<0,故③错误;
∵函数图象过点(-1,0),即x=-1时,y=0,
∴a-b+c=0,
∵b=-2a,
∴a+2a+c=0,即c=-3a,
∵抛物线与y轴的交点在(0,2)和(0,3)之间(不包括端点),
∴2<c<3,即2<-3a<3,
解得:-1$<a<-\frac{2}{3}$,故④正确;
综上,①②④正确,
故选:C.
点评 本题主要考查二次函数图象与系数的关系,掌握①二次项系数a决定抛物线的开口方向和大小.②一次项系数b和二次项系数a共同决定对称轴的位置.③常数项c决定抛物线与y轴交点.④抛物线与x轴交点个数取决于b2-4ac的值是解题的关键

练习册系列答案
相关题目
13.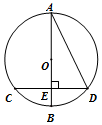 如图,在⊙O中,直径AB⊥CD于点E,AB=8,BE=1.5,将$\widehat{AD}$沿着AD对折,对折之后的弧称为M,则点O与M所在圆的位置关系为( )
如图,在⊙O中,直径AB⊥CD于点E,AB=8,BE=1.5,将$\widehat{AD}$沿着AD对折,对折之后的弧称为M,则点O与M所在圆的位置关系为( )
 如图,在⊙O中,直径AB⊥CD于点E,AB=8,BE=1.5,将$\widehat{AD}$沿着AD对折,对折之后的弧称为M,则点O与M所在圆的位置关系为( )
如图,在⊙O中,直径AB⊥CD于点E,AB=8,BE=1.5,将$\widehat{AD}$沿着AD对折,对折之后的弧称为M,则点O与M所在圆的位置关系为( )| A. | 点在圆上 | B. | 点在圆内 | C. | 点在圆外 | D. | 无法确定 |
20.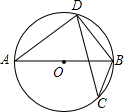 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
 如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )
如图,⊙O中,AB是直径,CD是弦,若∠ABD=55°,则∠C等于( )| A. | 25° | B. | 35° | C. | 45° | D. | 55° |
 如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.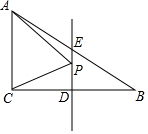 如图,△ABC中,∠ACB=90°,∠B=30°,AC=4cm,P为BC边的垂直平分线DE上一个动点,则△ACP的周长最小值为12cm.
如图,△ABC中,∠ACB=90°,∠B=30°,AC=4cm,P为BC边的垂直平分线DE上一个动点,则△ACP的周长最小值为12cm.